Virtual Mathematics
In quantum physics, we are used to refer to the inner states of some system (the points of the configuration space) which are never observable in any direct manner, so that the only way to guess about their presence is to interpret the outer behavior of the system the right way: the observable sequence is organized as if there were such inner states interacting in a definite way. Still, nothing prevents us from computing the same observable effects using an alternative technique that would not require any idea of the formerly introduced virtual states. This is a regular situation: in everyday life, we often produce the same from different components, using all kinds of tools; so, why not build a quantum system on a different basis?
There are mathematical analogs of this virtuality, and most often they are related to the formal manipulations outside the region of their applicability. Fundamental mathematicians prefer to ignore any objective foundations, pretending that mathematical constructs exist on themselves regardless of any possible applications. This is nothing but fantasy, or self-delusion. Every mathematical theory presumes a definite universe to support the abstract forms of a certain class. A rigorous derivation cannot mean anything but the elements of its object area, so that reasoning about any outer objects would be a logical fallacy. Nevertheless, in a purely formal manner, we can introduce objects that are impossible (virtual) in that particular theory, as a good occasion for passing to a different (extended) theory incorporating such abstractions along with the other objective features.
For example, adding up two natural numbers, we obtain a natural number that is greater than any of the original items. That may be interpreted as the (virtual) presence of these items in the sum as its inner components. Fancy a theory knowing nothing beyond even numbers (which will therefore constitute its universe, the object area). In this theory, a representation of an even number with a sum of odd numbers is closely resembling the idea of a quantum amplitude as a superposition of some virtual basis states. Going yet farther, we can admit the existence of such entirely exotic entities as negative numbers that will diminish any original item in addition. However, as soon as we learn to produce things representing these fantastic creatures, one can raise them to the class of observables and consider all kinds of integers together.
Similarly, a product of positive integers in a positive integer; taken together, all such numbers form the object base of one of the most important mathematical theories, where the operation of expanding an integer number in a product of integers plays a most fundamental part. Every natural number is then representable with a cloud of virtual products. There are "prime" numbers that reduce that virtual cloud to minimum; they provide a kind of a basis for the whole universe. For each number, its inner structure can be described by a sequence of the "level sets" Ln containing all the products with n components (from which we exclude the unity factor 1 since it, in fact, only specifies the scale, the units of measurement). The first level will obviously contain only the original number, while the lower level are absent for primes. Denoting the number of elements (the measure) for a set X as μ(X), we can introduce the index of a natural number N as
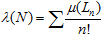
For any prime number, this value obviously computes to 1; all the other numbers will produce values greater than unity. For instance, λ(15) = 1.5, and λ(12) = 3.5. The order of components in the product is important, but here, we do not distinguish equal factors (admitting that a different definition might be useful elsewhere). The factorial weighting has been introduced from real life considerations: the variants of less lengths are more practical, producing the same thing with minimum effort. The index could characterize the hierarchical complexity of a natural number; on the other hand, it is related to the practical "productivity", since a number with a greater index can be obtained in many alternative ways. Given the expansion of a natural number into the product of primes, one cam easily calculate its index; however, the expression is no too trivial, which brings up observable effects similar to quantum interference, mixing the different inner representations (reaction channels).
Just like in the above additive example, virtual negative numbers could be introduced as well, possibly treated as positive numbers multiplied by the "negative unit" factor (–1) similar to common dimensional component (+1) in all the positive integers. The "physically allowed" virtual trajectories will therefore be restricted to the product expansions with the even number of negative contributions; alternatively, one could say that negative dimensions (factors of –1) in the positive nature can only be born in pairs (like the poles of a magnet). A considerable mathematics can be developed about such multiplicative universe, with nontrivial generalizations of the index theory.
The transition to the theory of all the integers will virtually retain this complexity; still, it may no longer be that significant, considering the highly symmetric nature of the general algebraic structure arising from the assumption that negative numbers can be "observable" on themselves (that is, they can be represented with some palpable things.
Similarly, in the theory of real numbers, no computation can be considered as "physical" unless it is going to produced a read answer. The introduction of the imaginary unit as 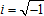 is an obvious violation of the domain of the square root function; however, complex-valued expressions are quite admissible as virtual paths, provided we get something real in the end. Here, the analogy with quantum virtuality is much more pronounced: the same real number can be approached by many paths in the complex plane, so that every real number becomes a hierarchy of complex loops, or cycles; a similar introduction of the hierarchical complexity index allows to develop an extensive mathematical theory. In the presence of constraints, the topology of the object area becomes more complicated, and the existence of at least one cycle (albeit of the zero length) can no longer be guaranteed. The virtual character of the imaginary unit within the real-number theory is also a kind of constraint limiting the collection of the admissible paths. On the other hand, such a theory could consider some alternative topologies of the complex plane not employing the traditional operations of complex addition and multiplication. Still, if we are going to build a uniform theory of complex numbers, we will need to fix the appropriate rules thus choosing one of the possible (though irreducible to each other) structures. is an obvious violation of the domain of the square root function; however, complex-valued expressions are quite admissible as virtual paths, provided we get something real in the end. Here, the analogy with quantum virtuality is much more pronounced: the same real number can be approached by many paths in the complex plane, so that every real number becomes a hierarchy of complex loops, or cycles; a similar introduction of the hierarchical complexity index allows to develop an extensive mathematical theory. In the presence of constraints, the topology of the object area becomes more complicated, and the existence of at least one cycle (albeit of the zero length) can no longer be guaranteed. The virtual character of the imaginary unit within the real-number theory is also a kind of constraint limiting the collection of the admissible paths. On the other hand, such a theory could consider some alternative topologies of the complex plane not employing the traditional operations of complex addition and multiplication. Still, if we are going to build a uniform theory of complex numbers, we will need to fix the appropriate rules thus choosing one of the possible (though irreducible to each other) structures.
Yet another example: negative and complex sets in a theory, where each set is associated with the ways of its virtual production, construction from other sets.
In the exactly the same manner, non-traditional logical theories could be developed, with the classical truth valuation obtained on the basis of non-classical reasoning.
In general, any branch of mathematics admits both classical theories, as working exclusively with the objects definable within the theory, and various "quantum" extensions accounting for the different modes of virtualization.
Dec 1982
|