The Quality of Negation
As philosophers declare, the primary purpose of the human (or any other) reason is binding the world together, connecting things that can in no way get connected otherwise. If so, the traditional mathematical habit of interrelating seemingly different entities should be respectfully appreciated as a part of the common productive work. Life gives many examples of how the tricks of one branch of industry perfectly match the needs of another; the mathematical language may come quite handy for sharing such fundamental schemes, and its practical importance is beyond any doubt. Still a sober attitude to the available resource is no less valuable. We are a part of the world, and any reflection of that whole in powerful abstractions, however accurate, is bound to remain partial; no formal construct can pretend to an unreserved universality. That is, our ability to tie one mathematical object to another, up to eliminating any distinction at all, can never guarantee that these entities would not accidentally get stuck in an entirely new environment requiring a clear awareness of their difference, and hence a different mathematics, albeit envisaging a quite decent retirement for earlier theories.
On the other hand, the multitude of peculiarities cannot appear but on the background of the primordial universality of the world, as there are no other worlds, and (therefore) no way out can ever open. In human practice (including mathematics), this results in the hidden presence of the sprouts of the future in the present and the past; every incidental guess reveals something that has long since been existing in the culture without attracting too much attention, silently waiting for its hour to come. Hence the typical technology of a scientific discovery: take a most plain and banal experience that would not even deserve mentioning in a good company, and pin up a couple of miserable subtleties that might eventually become great and meaningful. Those who are too lazy to format it as an academic hit may prefer the roads of the commonly known, with just a few philosophical deviations.
Well, here too, let us take a perfect commonplace and wonder if there is some underestimated creative potential in there.
Ask a not-yet-born baby ripening in a womb: two minus three, how much is it? You'll get a prompt answer: minus one, of course! Our lazy philosopher comes to press on with a real stumper: and what's that, minus one? The under-baby, scratching its head with a navel-string, thoughtfully mumbles: well, it's a kind of number... a negative ... exactly like one, but with the minus sign. This is enough to conclude that we are talking to a future mathematician: the lay people are ordinarily devoid of such clarity of the mind. Most would call this subtraction exercise improperly posed: it is not allowed to subtract a greater number from the lesser. Some would concede to the school answer (of minus one), with an explicit reservation that such numbers do not really exist, referring to sheer convention oriented to meeting a substantial enough positive individual, to clutch on him and diminish by an appropriate amount. In natural languages, being negative is invariably associated with something bad and wrong, some crazy dysfunction that should not normally happen. And, of course, there is an ancient profession whose representatives are firmly convinced that there are no negative numbers at all, and all we may deal with is positive records in the books, entries on a number of accounts split into the pairs like "we have — we need", or "sums due — payments to receive"; active and passive records are distinguished accordingly: fortune estimate vs. accumulated debt.
It is bluntly stupid to ask about the truth of all these viewpoints; each is certainly right, within their specific experience, and each requires as specific mathematics. In the pre-scientific times, it was commonly accepted that any particular thing can be characterized with a bunch of distinctive qualities, so that quantitative distinctions could be discussed within each quality. That is, first decide on whether it is in there, or it is not, and then inquiry for how much, where there is some. The absence we denote as null, while the present quantity can be numerically expressed as soon as some units of measurement have been fixed; the number 1 refers to the chosen scale for the specific dimension. An ancient geometer knew for sure that a line segment possessed some length, which did not depend on the mode of construction and the spatial orientation. Similarly, figures have area, and bodies have volume; when there is nothing measurable, the notions of length, area and volume are no longer applicable, and their usage amounts to a logical fallacy.
With all that, people do not live by the present moment; they think about the past and the future. The past feeds memories; the future makes plans. One is free to judge in an emotionally human manner, regretting the absence of the former glory or impalpability of things to come. This sorrow is referred to in mathematics every time we put down the minus sign.
An important note: compared to mere expression of the absence of something, the idea of the negative is a drastic step forward. No mere nothingness, but rather a kind of presence, albeit in an ideal way, inside the subject (or in any physical bodies, as an imprint or possibility). Obviously, such an ideal existence is somewhat different from real presence, and one should not confuse the two, lumping positive and negative experiences together. They are measured in different units. Nevertheless, they also have something in common: the very air of definiteness, qualitative homogeneity, and hence measurability. Which means that the uniform treatment of the positive and the negative is justified by their similarity in a certain respect, that is, in the context of a specific human activity, as long as we do not run off at the mind and disregard any distinctions at all.
To moderate our math and avoid too formal an attitude to the problem, there are well-proven formal tricks. One of them amounts to the already mentioned separation of the debit/credit kind, which directly makes practically different things also theoretically different. The debit and the credit are opposites, and one negates the other, but this negation is no longer merely quantitative, as it combines different qualities. Somewhere else, for the higher management staff, there is no difference, with one big bulk directly subtracted from another. Still, this is a faraway view, while operative accounting is to deal with the old two columns in the book. Once again: this is not a relic of primeval primitivism, or a moss-frown tradition; this is how the world goes round. Thus, biologically, everybody has a father and a mother; still, some children are brought up by a single mother, so that one parent is missing and comes with the negative sign; however, this differs from the actually having a single parent (for instance as in instance of parthenogenesis). That is, 2–1 is qualitatively different from the plain unity. It is only for school mathematics that all's the same.
In this line, monitoring resources will put everything that has ever come on the positive side as a present-tense fact. However, a part of that income has probably been partially consumed and is only present in memory; this is a past-tense negativity. Further, our current needs form a future-tense minus, that can significantly overweigh the present abundance. Note that positive numbers basically refer to the objective state of things, while negative contributions relate subjective feelings (at least within a single level of hierarchy); this may justify the position of those who consider negative numbers as merely conventional.
To account for conventionalities, a mathematician can represent a "generalized" number s with a cortege of two components ⟨a, b⟩, where a and b are non-negative real numbers (as presumably well-definable). The components a and b give, respectively, the positive and negative part of the number s which will conventionally be referred to as an additively split real number, or simply a split, to save space an the reader's effort.
Can we find anything like that in the history of mathematics? At every corner! For instance, rational numbers are traditionally introduced as pair of integers, with the rules of combining the components adjusted to our vision of the ordinary arithmetic. Similarly, complex numbers are defined through their real and imaginary components, with an appropriate specification of arithmetic. If so, why shouldn't we follow the same well-beaten track to play with real negation?
Treating the components of the cortege as the coordinates of a point in the plane, we effectively chose the positive and negative unity as the basis vectors of this space, denoting them as (+1) and (–1) respectively. Here, formally, (–1) is a monolith pictogram for some measurement unit, which may have nothing to do with the units used in the positive scale. Conversion of one unit to another will require an appropriate dimensional factor.
By analogy with complex numbers (and linear algebra), a quasi-algebraic notation could be employed: s = a + (–1)b, with the basis vector (+1) traditionally omitted for brevity, but always implied. A minimal list of useful features of real splits could be illustrated by the table below, where the complex-plane analogs are shown as well.
splits complex numbers

Of course, from the formal aspect, these equations are interdependent; however, our purpose is to stress the core of the approach, rather than adhere to rigor. Anyway, a deductive arrangement is entirely dependent on the strategy of arithmetization; for one possibility, one could depart from the algebra of splits with no reference to their inner structure (corteges and components); the positive and negative parts of a split will then appear in theory as functionals (mapping the space of splits into the space of positive reals), or as projectors (establishing correspondence between different splits). Since we keep on the tradition of building complex numbers over the real field, the negative unity naturally penetrates the rules of complex arithmetic. Still, nothing prevents us from defining (–1) as i2; in this case, the behavior of splits is to be derived from complex numbers.
Since the non-negative real axis is already well-ordered, all splits can be divided into two classes: those with a > b (Pos s > Neg s) are called positive; those with a < b (Pos s < Neg s) are called negative. This definition does not imply any direct combination of the components; geometrically, we mean the subdivision of the whole space of splits (the first quadrant of the Euclidean plane, the area (+|0|–) in the figure below) into separate subspaces, lying above or below the main diagonal (0|z). Any other subdivisions for all kinds of practical purposes are as contrivable.
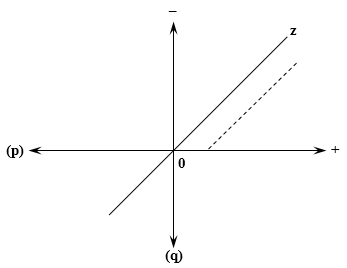
In the algebraic notation the negative unity (–1) may acquire the meaning of an operator (commonly known as negation) producing splits from other splits by the simple rule: the positive and negative parts of the split get interchanged. Graphically, this means reflection with respect to the main diagonal; in particular, the points of the axis (0|+) thus get mapped into the points of the negative axis (0|–). In the same manner, the positive unity can be treated as the operator of identity leaving each point as it is. In the component system, the positive unity is represented by the cortege ⟨1, 0⟩, and the negative unity by the cortege ⟨0, 1⟩. However, the (positive or negative) unity as an operator differs from the corresponding unit vector; negation as an action and as an action's result means different entities.
The transition from the component representation of splits to polar coordinates is formally the same as with complex numbers:
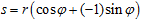
This layout may be useful to discuss certain intricate structural aspects; however, its justification can only come from a particular choice of relevant symmetries and metric. As we know, the traditional symmetries of the complex plane essentially differ from those of real splits. This is obvious from the very fact that splits are define in a single quadrant of the plane, so that extending theory to the whole plane would require introduction of yet another pair of unit vectors (for instance, p and q), as shown in the figure; thus generalized splits would then be formally written as a+(–1)b+px+qy, which resembles the quaternion structure. Imposing additional symmetries will "glue" some points together, folding the space in a specific manner. For common real splits the fundamental symmetry is
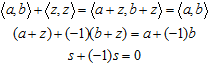
where z is a positive real number. Graphically, this identifies all the points of the main diagonal, and any straight line parallel to the main diagonal forms a class of equivalence, effectively collapsing into a single point. The complex-plane analog
c + i2 c = 0
is quadratic in the imaginary unity, which naturally leads to the usual quadratic metric. By analogy with the orthogonality of vectors in the Euclidean plane related to the zero value of their scalar product, the equation 1 + (–1) = 0 could be interpreted as a kind of additive orthogonality of the positive and negative dimensions.
Any symmetries of a general system (or the imposed constraints) will often diminish the number of its degrees of freedom, thus changing the effective dimensionality. For splits, we formally reduce the two-dimensional (or even four-dimensional, as in the "quaternion" extension) picture to a single dimension; this is an essentially nonlinear operation akin to projection. There are other types of projections, like the extraction of the positive or negative (real or imaginary) part, calculating the (quadratic or linear) norm, determining the phase etc. In ordinary life, we always observe any system in one of the possible projections, so that the existence of the others is to be somehow deduced. This is exactly like the choice of the gauge in relativistic physics. The unavoidability of projections is related to the complexity of inner motion; however, the symmetry of this unobservable behavior is determined by what we really can do with the system, and what is to be considered as the outcome.
The effective one-dimensional structure of the globally symmetrized splits should not deceive anybody: equivalence does not mean absolute identity. The bunch of straight lines parallel to the main diagonal is not the same as a collection of points in a single line, and there is still the qualitative distinction of the shifts up and down from the main diagonal (the regions with a < b or a > b).
Under the global symmetry (equivalence), for any split s, there is a unique equivalent "reduced" split R(s), such as either Neg R(s) = 0 or Pos R(s) = 0 (the positive and negative reductions). A linear order on the entire space of splits could be introduced, agreeing that any positive split is greater than any negative, and the positive and negative subspaces are independently ordered by the increase of Pos R(s) and the decrease of Neg R(s), respectively:
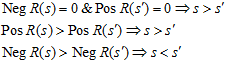
Consequently, the positive real axis can effectively be continued into the negative domain, which may look like transition from the two-dimensional picture to a single dimension. Graphically, the first quadrant is thus effectively expanded to the upper half-plane, with reduction being visualized as projection onto the horizontal line (–|+):
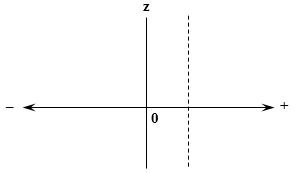
Still, these formally defined positive and negative branches yet remain separate and independent. Yes, each can be mapped onto the other, retaining the algebraic structure within the subspace; however, it is not quite evident how operations between the elements of different subspaces are to be introduced, to make the entire combined space uniform enough. One can easily observe that
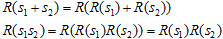
While multiplication of reductions keeps within the same straight line, adding together reductions of the opposite sign will certainly violate this simple structure, and one has to recourse to yet another reduction. That is, constructing the completely coupled field of real numbers implies rather strong assumptions that do not necessarily conform with the nature of applications.
A too straightforward interpretation of the quasi-algebraic notation for splits (or complex numbers) may lead to confusion, as the qualitatively different objects get treated on the same grounds. It is important to remember that the character combination s = a + (–1)b is only a different graphic expression for s = ⟨a, b⟩; the characters a and b refer to real numbers, (–1) points at the position in the cortege, while the plus sign means nothing but considering the two parts together. To produce an algebraic expression proper, one would write something like
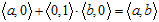
Similarly, in the right-hand side of the algebraically interpreted constraint s+(–1)s = 0, the character 0 does not stay for real zero, but rather for the cortege ⟨0, 0⟩, so that
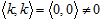
The placement of the positive and negative axes on the same straight line does not change anything in that respect, while rather hiding and disguising the (additive) orthogonality. An analogous symmetry exists for rational numbers represented with the corteges of two integers:
⟨k, k⟩ = ⟨1, 1⟩
since we can cancel the common multiplier in the numerator and the denominator of the ratio. Something like that can also be written for complex numbers brought to polar coordinates, ⟨x, y⟩ → ⟨r, φ⟩. In the absence of ramification, there are two conventional symmetries
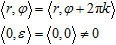
for any integer k and real angle ε. However, these symmetries may be violated in certain cases, so that a significant phase shift can bring us onto a different branch, and approaching zero from different directions can result in different limit values.
To summarize, in any theory, null (as an origin of a scale) and none (as negligible quantity) refer to the absence of a specific quality rather than to the absence of anything at all. In other words, there is no zero in general, there are many qualitatively different zeros. That is why, under certain assumptions, we can extend operations with the objects of the same kind and include the corresponding zero object in the elementary base. With all that, a rigorous mathematics would not treat zero as a number (or any other singular object), but rather as a mode of object production, something generic: a pattern, a scheme, a template, a type, the class of objects as the expression of the very possibility of their differentiation. Thus, the symmetry ⟨k, k⟩ = ⟨0, 0⟩, which can be interpreted as the equivalence of the point of the main diagonal, can also be turned inside out to describe the emergence of virtual pairs from null resembling the physical vacuum (which is far from being a sheer emptiness!). Pulling out a particle from the vacuum, we also create a hole of the same kind and size. Just like in physics, the zero level may often be movable; however, this symmetry does not influence the shape of the system in respect to the others.
In the same way, infinity is not a number (albeit fancied as infinite cardinal or ordinal), but rather the very activity of distinguishing the opposites and translating one into the other. Zero is related to infinity like the possibility of a product is related to actual production. A computer program is not the same as its execution; however, programming languages always account for hardware architecture, as well as hardware gets gradually adapted to language idioms.
Note that the special role of the null has to do with the logic of theory. Thus, one can assert the truth of a statement (+1), or its falsity (–1); either of these values is logically definite, assuming the possibility of verification (or falsification). On the contrary, the zero value will rather mean that the problem has been ill-posed, as the categories of truth and falsity are no longer applicable to the case (though the same statement, in this context, may allow positive or negative evaluation in some other respect, for instance, being correct or incorrect).
In the theory of splits, zero components stay for the absence of any operations on the positive or negative side, "debit" or "credit". Considering some inevitable overhead, the cortege ⟨0, 0⟩ is not fully replaceable with a virtual exchange ⟨k, k⟩ (writing off the same amount as placed to the account). Such operations may be nontrivial when the units of the positive and negative components differ (say, like in currency exchange). However, in classical bookkeeping, movements like that are often implemented as a pair of reductions ⟨a, 0⟩ и ⟨0, b⟩ put on different accounts, instead of the split ⟨a, b⟩. The distinction of the two technologies resembles the difference between correlated quantum transitions and cascades; the interference of virtual processes may result in clearly observable ("macroscopic") effects, but any financial speculation is organized in exactly the same manner! On a higher level of hierarchy, in consolidated reporting, the formal addition of movements recorded on different accounts is admissible:
⟨a, 0⟩ + ⟨0, b⟩ = ⟨a, b⟩
Yet another level involves a positive or negative reduction (or the zero balance).
The profound mathematical (and philosophical) sense of splits is due to the fact that every object can be produced in many ways, which may be considered as equivalent in some respect, while revealing some important differences in another context. Here, additive real-number splits have been discussed for illustration: every number can be virtually represented by a difference of two other numbers. Multiplicative splits are structured in the same way, as any real number can be treated as a fraction; such splits become additive in a logarithmic scale. Similarly numbers can be split into sums or products (possible infinite). Just take the example of the decomposition of any integer into a product of primes, forming the core and purpose of the classical number theory. More examples: rotation in the opposite directions, the difference of outer and spinor dimensions, layered manifolds... Finally, the very complementarity of the object and the subject in the context of a definite activity is of the same split nature. Since every activity is to reproduce its product on a regular basis, splits can be understood as loops, cyclic paths. Obviously, many-component and many-level splits are as feasible. In the general case, any mathematical object implies a hierarchy of all the possible splits, the modes of definition. The expansion of this hierarchy into an admissible hierarchical structure is known as a mathematical theory. The direction of this development is always suggested by the practical considerations, coming from the current human needs. Mathematics (as any other science) serves people to assimilate some formal techniques, the typical schemes of activity, to free our reason from the routine operations for striving to the yet unexperienced.
Dec 1983
|