Качество отрицания

Как учит философия, главное назначение человека разумного — связывать мир воедино, соединять то, что без нас никаким образом соединиться не может. Поэтому обычные в математике сопоставления одного с другим — часть разумной работы. По жизни часто оказывается, что навыки из одной отрасли производства прекрасно работают в другой, — математический язык для фиксации таких фундаментальных схем бывает очень удобен и потому безусловно важен. Однако трезво оценивать имеющиеся возможности тоже небесполезно. Поскольку мы лишь часть мира — сколь угодно полное представление его в наших абстракциях остается всего лишь частичным, и ни одна из формальных конструкций не вправе претендовать на безоговорочную универсальность. В частности, если удалось связать пару-тройку математических объектов, вплоть до полной практической неразличимости, это никоим образом не означает, что они не пожелают в какой-то ситуации вспомнить о своих различиях, и потребуют другой математики, — при всем уважении к традициям.

С другой стороны, разнообразие частностей возникает на фоне исконной уникальности мира: никаких других миров нет и (следовательно) быть не может. В человеческой практике (включая математическую) это означает скрытое присутствие зачатков будущего в прошлом и настоящем: если мы до чего-то додумались, оно существовало и в прежних представлениях — но до поры не привлекало внимания. То есть, типовая технология научного открытия — взять что-нибудь до боли знакомое, о чем приличные люди в обществе не разговаривают, — и указать маленькие тонкости, которые при случае станут исполнены великого смысла. Кому лень оформлять такие открытия — могут ограничиться предварительными замечаниями, полностью в русле общеизвестного — но с философскими экскурсами.

Вот и давайте возьмем нечто совершенно заурядное и посмотрим, нельзя ли углядеть в нем недооцененный творческий потенциал.

Если еще не рожденному младенцу в утробе матери задать вопрос: сколько будет два минус три? — он не задумываясь ответит: конечно же, минус один! Ленивый философ тут же подбрасывает вопрос на засыпку: а что такое минус один? Младенец чешет пуповиной в затылке и мычит: ну, это число такое... — отрицательное, — вроде единицы, только с минусом. Тут мы догадываемся, что беседуем с будущим математиком: люди обыкновенные, как правило, лишены подобной кристальности понимания. Многие сочли бы задачку на вычитание некорректно поставленной: нельзя из меньшего вычесть большее! Другие согласились бы со школьным ответом (минус один) — но с добавлением, что таких чисел на самом деле нет, это чистая условность, в расчете на то, чтобы когда-нибудь пристроиться к достаточно положительному числу — и уменьшить его в разумных пределах. В естественных языках отрицательность прочно ассоциируется с дурным и неправильным, с болезненным извращением, — чего в норме быть не должно. Наконец, есть древняя профессия, представители которой глубоко убеждены: никаких отрицательных чисел нет, а есть реальные количества по разным счетам, каждый из которых представлен парой: у нас есть — нам нужно; или, иначе: мы должны — нам должны. Соответственно, различаются активные и пассивные счета, оценка состояния — или долгов.

Глупо выяснять, кто из них ближе к истине: правы все — но каждый в пределах своего опыта. И каждому своя математика. В донаучную эпоху признавали, что любая вещь обладает букетом разных качеств — а в пределах одного качества можно говорить о количественных различиях. То есть, сначала: есть или нет, — а уж если есть, тогда сколько. Отсутствие мы обозначаем нулем; для наличного выбираем единицы измерения — и все сводим к принятой шкале; по каждому измерению, число 1 ссылается на выбранный масштаб. Античному геометру заранее ясно: у отрезка есть длина, и это не зависит от того, как и в каком направлении мы его откладываем. Точно так же, есть площади фигур и объемы тел; когда чего-то измеримого нет — понятия длины, площади или объема просто неуместны, и говорить о них — логическая ошибка.

Однако люди живут не одним мгновением: у них есть прошлое и будущее. О прошлом — память, про будущее — планы. И можно подойти к вопросу по-человечески эмоционально, сожалея, что былой славы уже нет, а чего-то очень желательного — пока нет. Эту грусть мы и обозначаем в математике знаком – (минус).

Важный момент: по сравнению с простой констатацией отсутствия, отрицательность — серьезный шаг вперед. Не ноль, а таки наличие — но идеально: в субъекте, или в других телах (как след или возможность). Понятно, что такое бытие несколько отличается от настоящего, и смешивать их в одну кучу, вообще говоря, неправильно. Единицы измерения у них разные. Однако есть и общее: сам факт качественной определенности, и потому — измеримости. Значит, можно в каком-то смысле (то есть, в контексте определенной деятельности) уподоблять положительное отрицательному и рассматривать их как явления однопорядковые. Разумеется, если не зарапортоваться и не отринуть напрочь всякие различия.

Чтобы держать себя в рамках и не допускать излишне формального отношения к делу — есть проверенные формальные приемы. Один из них — то самое разведение дебета и кредита, подчеркнутое различение того, что по жизни различно. Дебет и кредит — противоположности, одно отрицает другое; но это не количественное отрицание, а противопоставление разных качеств. Где-то в другом месте, для высшего руководства, — оно без разницы, и можно одну большую кучу вычесть из другой. Но это вид издалека — а в живой бухгалтерии надо честно записывать в два столбика. Еще раз: это не дикий примитивизм, не замшелая традиция, а точное отражение реалий бытия. У каждого есть отец и мать — это плюс; кого-то поднимала мать-одиночка — и одного родителя не хватает, он с минусом, — но это вовсе не то же самое, что фактически иметь только одного родителя (например, при партеногенезе). То есть, 2–1 качественно отличается от простой единицы. А школьной математике все едино...

Точно так же, при подсчете ресурсов: в плюсе у нас все, что когда-либо поступало, — это факт настоящего времени. Однако часть из этого уже израсходована и присутствует только в памяти — это минус прошедшего времени. С другой стороны наши потребности — минус будущего времени, который может существенно перевешивать наличное изобилие. Заметим, что положительные числа характеризуют объективное положение вещей — тогда как отрицательные больше о субъективных переживаниях. По крайней мере, пока мы ограничиваемся одним уровнем иерархии. В этом смысле правы те, кто считает отрицательные числа всего лишь условностью.

Чтобы учесть условности, математик может представить "обобщенное" число s кортежем из двух компонент ⟨a, b⟩, где a и b — неотрицательные вещественные числа (которые мы предположительно определить умеем). Компоненты a и b мы называем, соответственно, положительной и отрицательной частью числа s — а его мы, для определенности, будем именовать аддитивно расщепленным вещественным числом (или просто расщеплением, ради экономии места и читательского внимания).

Было в математической практике нечто подобное? Да сколько угодно! Например, рациональные числа мы определяем как пару целых — с правилами комбинирования компонент, подобранными так, чтобы это напоминало обычную арифметику. Точно так же, комплексные числа мы определяем через действительную и мнимую части — опять же, с подходящей детализацией арифметики. Так почему с отрицательностью не пойти проторенным путем?

Если трактовать компоненты кортежа как координаты точки на плоскости, базисные вектора этого пространства называются положительной и отрицательной единицей, которые естественно обозначить символами (+1) и (–1); формально, (–1) — нерасчленимый знак для некоторой единицы измерения, вообще говоря, никак не связанной с единицей измерения положительной части. Перевод одних единиц в другие требует соответствующего размерного множителя.

По аналогии с комплексными числами (и линейной алгеброй), допустимо ввести условно-алгебраическую нотацию s = a + (–1)b. Базисный вектор (+1) здесь по традиции опущен (но всегда подразумевается). Минимальный набор полезных свойств вещественных расщеплений можно проиллюстрировать приведенной ниже табличкой, где также показаны аналогичные правила для комплексных чисел.

Разумеется, с формальной точки зрения, эти равенства не будут независимыми — но нас интересует суть дела, а не формальности. Что из чего выводить — зависит от принятой стратегии арифметизации; например, можно исходить из алгебры операций над расщеплениями и обойтись без отсылок к их внутреннему строению (представление кортежами): положительная и отрицательная части расщепления появятся тогда в теории как функционалы (отображения из пространства расщеплений в пространство вещественных чисел), или как отображения одних расщеплений в другие (проекторы). Традиционно, мы идем от вещественных чисел к комплексным; при этом отрицательная единица (–1) естественно возникает в равенствах комплексной арифметики. Однако ничто не мешает, наоборот, определить (–1) как i²; — и тогда арифметику расщеплений придется выводить из комплексной плоскости.

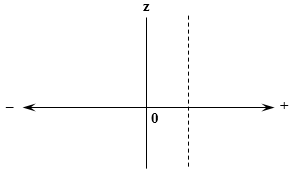
Поскольку на пространстве неотрицательных вещественных чисел уже задан порядок, можно разделить расщепления на два класса: при a > b (Pos s > Neg s), расщепление s называется положительным; при a < b (Pos s < Neg s), расщепление s называется отрицательным. Это определение никоим образом не предполагает прямого комбинирования положительной и отрицательной частей; геометрически, речь идет о разбиении пространства расщеплений (первый квадрант на обычной евклидовой плоскости; на рисунке — область (+|0|–)) на два подпространства (ниже или выше главной диагонали (0|z)). Разумеется, возможны любые другие подразделения, в зависимости от практических нужд.

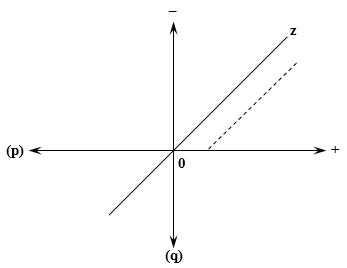
В алгебраической нотации отрицательная единица (–1) приобретает смысл оператора, (который мы называем отрицанием), однозначно переводящего одни расщепления в другие по определенному правилу: положительная и отрицательная части расщепления меняются местами; графически, это отражение относительно главной диагонали. В частности, точки оси (0|+) этот оператор переводит в точки оси (0|–). Точно так же, положительная единица как оператор просто переводит каждую точку в ту же самую. В компонентном представлении, положительная единица представлена кортежем ⟨1, 0⟩, а отрицательная единица — кортежем ⟨0, 1⟩. Однако единица как оператор — не то же самое, что единичный вектор; отрицание как действие и как результат — вещи разные.

Переход к полярной системе координат от компонентного представления формально одинаков для расщеплений и комплексных чисел:

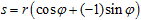
Такая запись позволяет обсуждать тонкие особенности изучаемых структур — однако оправдана она лишь там, где это отвечает набору наложенных на систему симметрий и выбору метрики. А традиционные симметрии комплексной плоскости сильно отличаются от обычной симметрии расщеплений. Это ясно уже из того факта, что определены расщепления только в одном квадранте плоскости, и для расширения на всю плоскость потребовалось бы (как показано на рисунке) ввести еще две фундаментальные единицы (например, p и q) и расщепление общего вида записывать как a+(–1)b+px+qy, — нечто вроде кватерниона. Дополнительные симметрии "склеивают" пространство специфическим образом, отождествляя его точки. В случае обычных аддитивных расщеплений предполагается фундаментальная симметрия

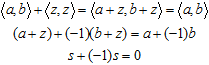
где z — положительное вещественное число. Графически, это отождествляет все точки главной диагонали — и любая прямая, параллельная главной диагонали, формально склеивается в одну точку (задает класс эквивалентности). Аналог из комплексной математики

c + i² c = 0

квадратичен по мнимой единице — что логично порождает квадратичную метрику. По аналогии с ортогональностью векторов на плоскости, когда их скалярное произведение равно нулю, можно трактовать равенство 1 + (–1) = 0 как своего рода аддитивную ортогональность положительной и отрицательной единиц.

Симметрии (наложенные на систему связи), вообще говоря, уменьшают количество степеней свободы, меняют эффективную размерность пространства. В случае расщеплений мы формально сводим двумерное пространство к одномерному (или даже четыре измерения склеиваются в одно, как для "кватернионных" расщеплений) — это существенно нелинейная операция, нечто вроде проекции. Существуют и другие проекции: например, выделение положительной и отрицательной (вещественной или мнимой) частей расщепления (комплексного числа), вычисление нормы (квадратичной — или по линейной комбинации компонент), вычисление фазы, и т. д. На практике мы всегда видим систему в одной из проекций, и существование других — надо восстанавливать умозрительно. В релятивистской физике аналогичную роль играет калибровка. Необходимость проекций связана с непосредственно не наблюдаемым внутренним движением. Однако симметрии этого "виртуального" пространства определяются тем, что мы реально умеем делать с системой и как регистрируем результат — что считаем готовым продуктом.

Эффективная одномерность пространства расщеплений с глобальной симметрией не должна вводить нас в заблуждение: эквивалентность не есть тождество. Совокупность прямых, параллельных главной диагонали — это нечто иное, чем совокупность точек на прямой, а сдвиги прямых вверх или вниз от главной диагонали (области с a < b и a > b) все еще качественно различны.

В условиях глобальной симметрии, для любого расщепления s существует единственное эквивалентное ему "редуцированное" расщепление R(s), такое, что либо Neg R (s) = 0, либо Pos R (s) = 0 (положительная и отрицательная редукции). Можно ввести линейный порядок на пространстве расщеплений, если положить, что все положительные расщепления больше отрицательных; при этом положительные расщепления упорядочены по возрастанию Pos R(s), а отрицательные расщепления — по убыванию Neg R(s):

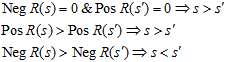
Следовательно, мы можем формально "продолжить" вещественную полупрямую в область отрицательных значений, эффективно переходя от двух независимых измерений к одному; графически это выглядит как развертывание первого квадранта в верхнюю полуплоскость, а редукция представляется проекцией на горизонталь (–|+):

Тем не менее, положительная и отрицательная ветви все еще остаются разными пространствами: да, одно однозначно отображается в другое с сохранением алгебраической структуры внутри каждого из пространств, — но заранее не очевидно, как определить алгебраические операции с элементами разных пространств, что позволило бы трактовать эти элементы единообразно. Легко видеть, что

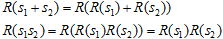
Умножение остается умножением и в редукциях — однако сложение отрицательных редукций с положительными выводит нас в нередуцированную область — и приходиться прибегнуть к еще одной проекции. Таким образом, построение единого пространства вещественных чисел требует достаточно сильных допущений — которые не всегда оправданы приложениями.

Слишком прямолинейная трактовка условно-алгебраической нотации расщеплений (или комплексных чисел) может легко ввести в заблуждение: качественно разные объекты трактуют на единых основаниях. Но запись s = a + (–1)b — это лишь другая графика для s = ⟨a, b⟩; здесь символы a и b ссылаются на вещественные числа, (–1) указывает на позицию в кортеже, а знак суммы говорит о совместном рассмотрении компонент. Чтобы превратить это в собственно алгебраическое выражение, следовало бы писать нечто вроде

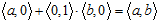
В частности, в правой части связи s+(–1)s = 0, понимаемой алгебраически, подразумевается вовсе не вещественный нуль, а кортеж ⟨0, 0⟩, так что

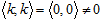
Расположение положительной и отрицательной полуосей на одной прямой ничего в этом плане не меняет, а лишь скрадывает (аддитивную) ортогональность. Совершенно точно так же, на пространстве рациональных чисел (представленных кортежами из двух целых чисел) действует симметрия

⟨k, k⟩ = ⟨1, 1⟩

поскольку мы можем сокращать числитель и знаменатель на общий множитель. Нечто подобное возникает в полярных координатах для комплексных чисел: ⟨x, y⟩ → ⟨r, φ⟩. При отсутствии ветвления, действует симметрия

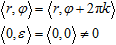
для любого целого k и любого угла ε. Но в общем случае для каких-то приложений эти симметрии могут не соблюдаться: сдвиг фазы на достаточно большие углы выводит на другие листы, а приближение к нулю с разных направлений может давать разные пределы.

Сухой остаток: во всякой теории нуль (как отметка на шкале) и ноль (как количество) — не отсутствие предмета как такового, а отсутствие определенного качества. То есть, нет нуля вообще — а есть нуль по отношению к некоторой единице, качественно определенный нуль. Именно поэтому мы можем (в каких-то допущениях) доопределить операции с объектами одного типа, включая в элементную базу того же типа нули. Однако в строгой математике, ноль вовсе не число (единичный объект); это, скорее, способ порождения объектов: шаблон, форма, схема, образец, тип, — то есть, класс объектов, характеристика самой возможности их построения. Симметрия ⟨k, k⟩ = ⟨0, 0⟩ может быть интерпретирована не только как эквивалентность точек диагонали, сведение их к нулевому кортежу, — но и в обратном смысле, как порождение виртуальных пар из нуля, который тогда оказывается подобен физическому вакууму (а это вовсе не пустота!). Если мы выдрали из вакуума частицу — в нем возникает дырка того же типа и размера. Как и в физике, нулевой уровень часто оказывается подвижным — но такая симметрия не меняет поведения системы в отношении прочих симметрий.

Точно так же, бесконечность — не число (хотя бы и кардинальное, или ординал), а та самая деятельность, в которой мы различаем противоположности — и переводим их друг в друга. Ноль связан с бесконечностью, как возможность и действительность; это одно и того же с разных точек зрения. Одно дело — компьютерная программа, другое — работа по программе; однако языки программирования исходят из возможностей железа, а железо понемногу адаптируется под идиоматику языков.

Заметим, что особая роль нуля связана с логикой теории: например, мы можем говорить, что некоторое суждение является истинным (+1) или ложным (–1) — но и то, и другое утверждает его логическую определенность, возможность проверки, — тогда как нулевая оценка означает, скорее, некорректность постановки вопроса, неприменимость категорий истинности или ложности в данном контексте (хотя в других отношениях то же суждение вполне может претендовать на положительную или отрицательную оценку: например, быть правильным или неправильным).

В теории расщеплений нулевые компоненты означают просто отсутствие каких-либо операций по "дебету" или "кредиту"; с учетом "накладных расходов", кортеж ⟨0, 0⟩ — совсем не то же самое, что виртуальный обмен ⟨k, k⟩ (сколько зачислили — столько же списать). Заметим, что операция обмена может быть нетривиальной, если единицы измерения положительной и отрицательной компонент различны: например, в случае обмена валюты. Однако в классическом учете обмены представляют не расщеплениями ⟨a, b⟩, а парой редукций ⟨a, 0⟩ и ⟨0, b⟩, отнесенных к разным счетам. Это различие подобно тому, как в физике мы различаем квантовые переходы и каскады; в виртуальных мирах возможна интерференция процессов, приводящая к вполне наблюдаемым ("макроскопическим") эффектам, — но точно так же устроена и финансовая спекуляция! На более высоком уровне иерархии, в сводных отчетах, оказывается возможным формальное сложение движений по разным счетам:

⟨a, 0⟩ + ⟨0, b⟩ = ⟨a, b⟩

Следующий уровень — предполагает положительную или отрицательную редукцию (или нулевой баланс).

Глубокий математический (и философский) смысл расщеплений состоит в том, что один и тот же объект возможно получать различными способами, которые в каких-то отношениях будут эквивалентными — но в другом контексте возникают серьезные различия. Здесь мы говорили об аддитивных расщеплениях вещественных чисел: каждое число виртуально представляется разностью двух других. Точно так же устроены мультипликативные расщепления, когда вещественное число представлено отношением двух чисел; легко видеть, что это расщепление становится аддитивным при логарифмировании. Можно обсуждать расщепления в суммы и произведения (в том числе бесконечные). Пример — разложение чисел на простые множители, ядро и смысл классической теории чисел. Еще примеры: вращение в разных направлениях, инверсия относительно окружности, различение внешней и спинорной размерности, расслоения многообразий... Наконец, из той же серии — противоположность объекта и субъекта в контексте определенной деятельности. Поскольку же любая деятельность регулярно воспроизводит свой продукт, расщепления можно понимать как циклы, замкнутые пути; соответственно, возможны многокомпонентные и многоуровневые расщепления. Любой математический объект в общем случае представляется иерархией всевозможных расщеплений — способов порождения определенности. Развертывание этой иерархии в одну из допустимых иерархических структур называется математической теорией. Способ развертывания — их практики, от насущных потребностей. Математика (как и любая наука) нужна людям для того, чтобы вооружать их формальными приемами, типовыми схемами деятельности, освобождая разум от рутинных операций ради поиска неизведанного.

декабрь 1983