Numeral Systems

Despite of the stubborn attempts of the apologists of "pure" science to detach mathematics from life, any mathematical solutions are only meaningful in the context of certain practical needs. Sometimes, it does not go much beyond preliminary exercise, similar to children's play; still, acquiring a sort of "activity mood" is most important to proceed to activity proper. Most mathematical results prove viable inasmuch as their parent forms of activity keep on somewhere in the hierarchy of the culture.

Just for illustration, a few well-known facts from the life of numbers.

We grew so accustomed to these little creatures that we just don't admit a thought about their origin and nature, as if they had existed long before the humanity's arrival to the Earth and would exist after it's gone. Yes, numbers express something objective, the essential in things that does not depend on whether anybody thinks of it or not. However, they are but a form of expression, the subjective view of objective quantities. Numbers come as a product of human activity, so that specific activities may lead to the different ideas of a number.

As in any science, mathematical forms either refer to the observable properties of things, or are produced in the inner development of science (theoretically), or are used to delimit the domains of the possible applications (as a typical experimental setup). In particular, a number may characterized the interrelations of different activities; this type of comparison is yet another activity called measurement, as one activity becomes a measure of the other. Measurement cannot produce just anything: on one hand, it is determined by the object, and on the other, we need a practical result rather than the process of measurement as such, which leads to a limited accuracy of any measurement within the range of reasonable sufficiency. That is, we approach the complexity of the world with a subjective scale, using the historically formed reference frames. When a scale is no longer satisfactory, we build yet another one, which does not eliminate any previous valuations to be held within the new estimates as the levels of approximation (or alternative pictures of the world). There is no need in "exact" values where some general judgment is enough. Moreover, certain scales may fail to go along with each other. Thus, Europeans usually distinguish four seasons of the year, while some people in Asia and Africa prefer to speak of five seasons (possibly of variable length). The both views reflect certain aspects of the objective reality; still, it would be rash to judge of European climate by African measures, and the other way round.

A typical measurement procedure is hierarchical: first, we develop a general idea of the scope; in the following, facts get sorted out according to some specific criteria; finally, we may need several degrees of refinement, subdividing the gross partitions into smaller portions. In mathematics, this process is reproduced in a specific activity, and we call its abstract product a system of numeration.

In general, a numeral system is a hierarchy of scales (gauges), so that any number (from a practically important range) could be represented by a collection of positions on the different levels. Conversely, given a collection of such valuations, we can organize our activity and tune the measurement system to produce exactly that numeric result.

There are no restrictions on the nature and structure of the possible representations. Each of them fits in an appropriate practical area. Similarly, the same number admits multiple representation, as it can be obtained in the course of very different activities. The issue of the equivalence of such different representations thus stops being a favorite mathematicians' toy and become a quite pragmatic question: where several activities are involved in an embracing activity, their results are objectively commeasurable. No such unifying activity, no sense in formally introducing any relations. In particular, formal constructions may service the activity of consciously rearranging production technologies; in this case, mathematical results will acquire a normative air: we do not merely adapt our behavior to reality, but rather dare to demand that reality agreed with our expectations, and we actively interfere with the affairs of the world to make it keep our environment within the suggested parameters.

For the moment, of all the common numeral systems, positional systems might be considered as the most universal, with the rest kept for mainly historical reasons. Time will show whether this viewpoint is viable. Currently, there is a certain trend towards more flexible positional representations; nobody warrants that no further generalizations shall come. In the traditional setup, a positional base K numeral system is associated with the ground scale constituted of the natural numbers {1, ... , K–1}, so that a (positive) result of some measurement could be represented by one of the numbers from this finite set (namely, the "closest" in the given context, in the sense of the current activity). If the quantity does not fall in the ground scale, we proceed to the next level of hierarchy, consecutively introducing scales of the type {K^p, ... , (K–1)•K^p}, with any natural p, for numbers greater than K–1, and the scales of the model {K^–q, ... , (K–1)•K^–q }, with natural q, for numbers below unity. Once an appropriate scale is found, the closest element of the scale is meant to be the first significant digit, while the corresponding number p or –q is referred to as the order of magnitude (or a position of the record; hence the term "positional system"). In many cases, knowledge of the orders of magnitude is enough for decision-making. Otherwise, we examine the difference of measured value from the first rough estimate. Provided the procedure of measurement is flexible enough, we can estimate this difference by the order of magnitude thus obtaining the next significant digit. In this way, any (measurable) number gets eventually represented by a collection of pairs {k, p}, or {k, –q}, where k is the first significant digit in the corresponding order. In general, the result of a measurement does not need to be represented in all the orders: each number unfolds its own hierarchical structure with a specific set of nonempty positions. Conventionally, it could be written as

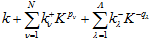
where each of the three parts may be missing. For convenience, the non-significant elements are commonly denoted by a special character, zero. One is to be clearly aware that zero is not a number; it only marks a vacant (void) position, just like in a payment order form, where the field for the total to pay is marked out by a row of empty cells to fill in. Nowadays, mathematicians tend to include zero in all kinds of numerical sets, with a lot of surprise at the freaks of the theory due to this logical laxity. Still, who would not be seduced? With a formal inclusion of the zero in the collection of admissible digits, we can rewrite (*) in a simple and attractive form:

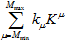
with the summation running over all M_min ≤ μ ≤ M_max, admitting that some positions are zeroed out. A convenient notation is a great thing; with appropriate conventions, some implications become just obvious. Nevertheless, any notation is designed for a certain class of activities, and it will limit the thought to that very class, up to obstructing scientific creativity with a pile-up of stereotypes.

Clearly, a positional system is best suited to representing rational numbers: any measured value can only be written as a finite sequence of digits (with a finite "accuracy"). When a mathematician urges us to fancy an infinite sequence, the magical words "and so on" are but a sheer emptiness unless we can indicate a specific activity to produce new members of that infinite row. In fact, infinity is beyond mathematics; this is a reference to an unachieved activity, the absence of the product. In the sense of our template scale, zero and infinity are the two complementary kinds of its inapplicability, for too small or too big numbers (meaning that, for practical reasons, we choose to restrict ourselves to linearly ordered scales).

Strictly speaking, the quantities of different levels are not comparable, and one has no right to bluntly sum them up. The sums in (*) and (**) are but a technical convention, a way to stress the hierarchical nature of activity and the corresponding scale. To literally understand such formulas is like add a bike to an orbital station: yes, Russian rubles can sometimes be converted to US dollars, but this requires yet another activity, with an in-built overhead. As our mathematics does not much care for formal discretion, one can use this super-democratic science to evaluate the level of public wealth by taking the average of the meager pennies of a pauper and a round capital of a multibillionaire, which is busily utilized by the bourgeois brain-washers.

With all that, we shall follow the tradition for a while, permitting hierarchies squeezed to a flat something, so that any numbers, regardless of their source, could be considered as comparable. Sensible abstractions make no harm. Things are getting rude where a sketch of a landscape is meant to be the landscape itself, and reasonable choice is to cede to despotic arbitrariness.

The notion of a limit is the next step towards more formality. We cannot sum up the whole infinity, to write down all the digits, accounting for every finer (or coarser) scale. Still, in many practically important cases, one can find that different hierarchical structures represent the same real object; in the context of positional systems, we speak of the levels of accuracy, holding in the mind the possibility of less trivial interpretations.

Naturally, any unity means the presence of a unifying activity. Traditionally, mathematicians compare two numbers written down in the same positional system and say that these numbers differ by less than K^M if their records coincide for all μ ≥ M. For negative M, this refers to the segments of the fractional part, so that the "exact" value could be defined as the limit at M→–∞. As one will readily guess, the segments of the integer part can be treated in exactly the same manner, and numbers can be compared by coinciding strings for μ ≤ M; infinite growth is in no way different from infinitely approaching zero. In hierarchical terms, we say that any sequences of digits coinciding between the levels M_min and M_max represent the same number in these limits. This does not prevent us from discovering differences in other limits; any equivalence is therefore relative, and a consistent theory must explicitly indicate the hierarchical structure supporting that particular way of identification. In modern mathematics, however, the domain of applicability is only implied, which stirs the temptation to declare a special result as a universal law, the ultimate truth valid for everybody for all times.

Practically, the existence of a limit means feasibility, that is, we can produce a particular product in a properly organized activity. Quantitative comparison of such products is a separate activity; if, for some reasons, one quantity cannot be expressed through another, this is not a mere formal irrationality, but rather an expression of certain objective arrangement of things. Practically comparable objects (the products of the same activity) must be mathematically comparable, provided an appropriate number system has been chosen. In other words, such things belong to the same scale hierarchy. Thus, the fraction 1/3 contains an infinite number of digits in the decimal notation; in the positional base 3 system, it has a finite representation, while the fraction 1/10 becomes an infinite sequence of digits. The commensurability of these quantities comes out when we consider the positional base 30 system, where the both fractions are finite. If the base 30 hierarchy happens to be unachievable (forbidden by some "selection rules"), no mathematics will allow comparison of ternary and decimal numbers in practice. Situations like that are well known to musicians, as the different musical pitch systems (scales, moods, tonalities, chords etc.) are not always compatible within the same composition.

In this context, the incommensurability of rational and irrational numbers only means that some numbers (characterizing the products of certain activities) cannot have a finite representation in a positional system with any natural base K. So, what? In the XX century, many alternative positional systems have been thoroughly studied, in particular, with a real base and real numbers for the "digits". The hierarchy of scales is in no way restricted to the clones of the same scale; in general, this is collection of "natural" (for a given object area) measurement units (which may differ at different levels), with the corresponding sets of compatible scales (selection rules). In physics, by the way, we normally adopt the unit systems that eliminate most dimensional factors in the formulas. The same policy is tenable in mathematics as well, as we demand that a consistent structure of a numeral hierarchy (a positional system) should reflect the hierarchy of the corresponding object area (the organization of activity). If a product of activity is practically feasible (obtainable in a finite time), its mathematical models will be finite as well, with an appropriate choice of the scale hierarchy. No limit convergence is needed any longer.

Mathematical incommensurability is an expression of the objective qualitative distinction. For instance, take a cylindrical volume (a "glass") with the base diameter 1 and the height 4; its capacity equals π. Now, take a rectangular volume (a "box") sized as 1´1´3, with the capacity of 3. Using one of the volumes, one can never produce the same quantity of liquid as using another. But, who can forbid us using both volumes in alteration, depending on the production necessity? The total quantity of liquid will then be expressible as a pair of numbers rather than reduced to a common scale: the number of glasses + the number of boxes. Here, the plus sign corresponds to a quite real operation of mixing the content in a volume of a high enough capacity. This closely resembles what we do in quantum mechanics, where a state vector of a two-level system is represented by a linear combination of the "pure" states, with the observables including the contributions of the both components. Reduction of many-dimensioned scales to a common base is only possible with some finite accuracy acceptable for a practical purpose. Provided there is a real procedure of generating finer approximation of that type, one can refer to it as approaching a limit. Still, there is no reason to believe that every aspect of the world is expressible in numbers, and even less, that a limit of a number series will necessarily be a number.

For an illustration, consider a positional system with a complex base Z = Kexp(iφ), |K|>1. Then Z^–m formally tends to zero at m→+∞, and one might fancy constructing fractions of infinitely increasing accuracy. However, as the phase factor exp(–imφ) is rapidly oscillating for higher m, the zero limit value of the amplitude corresponds to a continuum of the possible phase values, which is far from being a number. Different modes of approaching the limit will result in specific phase distributions.

Above, we only discussed the structural (static) aspects of numeral systems. In addition, one could also touch the system side proper, system dynamics: a general system is exactly the way of producing structures by other structures, so that some input would result in a certain output. Thus, we must be able, given a number, to construct its representation in the current positional system; on the other hand, we need to use a positional record of a number to direct our activity so that its product would be characterized by that very number. To get rid of such routine operations, humans invent all kinds of automata mechanically reproducing what once was a creative inspiration. Of course, the robot does not care for shifts in the world resulting from its operation. To assess the outcome, one needs a human. At least, we need to decide about the appropriate level of activity, which will shape out judgement of whether there is any result at all; it is only afterwards that we can get engaged in comparing the products. This nontrivial task gave birth to the huge edifice of the computation theory (including quantum computing). First, we gingerly examine the cultural heritage of the traditional computational techniques; eventually concocting a general principle, we start to dogmatically impose it all around as an a priori criterion of truth...

In the theory of generalized number systems (with real base and real digits), one finds a theorem stating that, for any choice of the base and digits, the representation of the complete real axis will be either ambiguous (some numbers will be represented by at least two sequences of digits), or incomplete (with some real numbers not representable in the chosen numeral system). This closely reminds the situation with the famous Gödel theorem about the logic of completeness and non-contradiction. The resemblance is not accidental; it is to stress once again that mathematics is essentially rooted in human activity, albeit squeezed in the narrow normative patterns, official standards, or public stereotypes.

Now, let us possess an automaton to feed in a (non-formal) number and (with a little patience and luck) catch an eventual outcome representing the number with a sequence of characters (the digits of the generalized numeral system). Since, traditionally, the collection of the digits is finite, one could somehow order and enumerate them; thus we come back to the natural-number representation with the digits from 1 to K–1, except that the number K is no longer taken for the base. On the next stage, we shall extend the original collection of digits adding any finite sequences of the ground-scale digits (possibly including zeros in some positions) as separate digits. Such fragments of a positional record are countably denumerable, and we can label them with natural numbers starting from K+1. These new digits are no worse than the original ones and we can consider numeration systems with (countably) infinite sets of digits corresponding to the possible states of our numeration automaton. This may be more technically handy, to avoid any commensurability issues; we never need to seek for common scales, since any rational number at all is representable in thus extended system with a finite sequence of digits. In the systemic picture, the machine calculates the positional representation of a number digit by digit and stops after a finite number of steps. The last output digit will be interpreted as infinitely repeated, since it will stay the same in all the subsequent checks (regular time moments). In particular, that last digit may happen to be zero; the traditional finite expansions are thus reproduced.

In this way, the issue of irrationality gets reduced to the typical question about whether the automaton, once put in motion, will stop at some step or not. A minimal acquaintance with computation theories hints that the problem does not have a formal solution. Instead, we get a hierarchy of complexity levels, with poorly understood (and sometimes poorly defined) interrelations. The worst of all, the very notion of a machine at rest can hardly ever be formally defined. Indeed, let the automaton stop operation and display the same output ever since. How do we know that it won't resume activity after a very long time? There are expansions with extremely long sequences of repeated characters. Can we claim to obtain the final result, or shall we wait? How long? A minute, a year, an eternity? The answer can only be practical: once we feel that something remains unchanged during a particular activity, we may consider it a constant, an axiom, or a rule (a law). Such an approach is common among physicists, speaking of those who did not yet go crazy about "accuracy" and "rigor" and make mathematical "truths" a religious belief. A factor in the integrand that is almost constant in the integration region can be boldly taken out, possibly replaced with an appropriate average. All we need is to decide something for the time being and proceed with the activity, rather than sit still with a vacant gaze upon the stupid machine. If our decision goes wrong, life will correct us where needed. Making errors is better than no making at all.

Our preliminary and scarce ideas of numeral systems are also bound to evolve in most unexpected directions. For instance, the uniformity of the scale at any level is highly questionable, and hence the notion of the base needs a thorough revision. We use a "mixed" scale every time we consult a watch. It seems quite expectable that, to measure something with on the different levels of accuracy, we will need as different technologies producing their native measures. Following the reflection rule, we'll need as diversified mathematical models.

Now, every hierarchy is qualitatively infinite, and one can always consider intermediate levels between any previously found. A numeration system does not need to be unfolded in a discrete hierarchical structure, in a sequential manner. That is, instead of the sum in (**), one might employ an analogue of the Lebesgue integral:

,

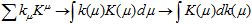with every distinction level K(μ) (a "position" in the current notation) introduced through a measure dk playing the role of a digit in that particular position.

Yet another generalization will drop power series expansions in favor of some generalized expansion base. For instance, one might try any set of orthogonal functions, like in a common Fourier series. Many exotic constructions go in the same row: exponential and factorial expansions, the binomial system, Fibonacci numbers etc. It is not evident whether some of these systems are practically justifiable, but they may well serve as yet another mathematical game (why not?). Just for fun, observe the strange reincarnations of the same positional record (a sequence of digits) in very different numeration hierarchies. In certain cases, such an amusement might grow beyond the game. Thus, a "spectral" representation of a number implies a definite sequence of "energy levels" summing up into a kind of "inner energy".

Finally, the persistent attention to the cultural roots of the numeral systems, their derivation form the human activity, will inevitably bring us to the idea of culturally determined scale hierarchies eliminating any arbitrariness. Once again, one might recall pitch system formation in music. The historical selection leaves us with stable and regular enough scales, suppressing any virtual fluctuations. Each scale is a discrete collection of continuous zones, implying a well-determined hierarchy of subscales, embedding some zone structures in the other scales in a logical manner. The possible ("permitted") musical forms depend on the structure of the fundamental scale, so that music written in a different mood will sound differently. This model illustrates the significant features of any activity; hence, the development of mathematics will gradually reveal such natural structures. Of course, the traditional mathematical constructs will stay; they are obviously useful in many applications. Still a sensible science would avoid both empty zeros and wild infinity.