Abstract Pictures
The science of mathematics (as any other science) is to reduce our daily problem to sheer formalities. And that's alright. Since, otherwise, we would get stuck in reinventing whatever has already been experienced, with no time for far-reaching creativity. However, as long as a human being is different from a bee, one cannot be completely satisfied with the efficient ways of being; there is an ardent desire to grasp the whole thing from elsewhere, from a neighboring universe. Which is commonly known as intuition. Just cultivate it, and the formalities are no longer restrictive, and no distance is too far to march.
Well, there are people and people. Intuition on one kind may be inapplicable to a person of another constitution. Some will enjoy the idea of a sequence of actions: the "Dao", so to say, the procedurality as such. With the funny pictures as an occasional result. Some others, on the contrary, would hate being too algorithmic: they prefer a visible thing, to look at it from every side and finally decide. Similarly, in music, there are both melody seekers and harmony feelers. The third way is related to instrumental intuition, practical sense, the ability of build it, picture it, and play it on the fly. Which is commonly known as talent.
Mathematicians have intuition of a special flavor. Any order is due to numbers; any picture are in the reign of geometry. Still, numbers tend to gradually turn into abstract structures, while geometry gets drowned in homeomorphisms and reduced to numerical (topological) invariants. The talent of math thus grows into logic, the sense of the essentials, the ability to withdraw from the particulars.
In real life, particularity is much more helpful. It's a pleasure, to discover still finer details, one by one. With all that, any subtleties are chaotic and dull on themselves; that is why we need to attach them to some solid principle, thus putting the ocean between firm coastlines that would justify any pain and trouble. With a bright and vivid abstraction, the storms are tender, and no calm is dead.
Alright, let us amuse ourselves a bit with browsing the fancy of visualized numbers.
Numbers are all different from each other, just like people. Quite naturally, everything begins with counting: one, two, three, four, five, I caught a fish alive; with a fish live indeed, I don't need to proceed... Why? Because the basic idea of the process is already clear: there is a certain direction to mark-up at some pace.
In the same manner, rational numbers are readily visualized as a couple of independent directions, with a specific pace along each. Something like a planar grid. Now, a practical fish breaks in and asks: what if we are going like that, but in the same direction? Will we come to anything common, or never? This happens to depend on the step size: for some combinations, there is a consensus, while some others give no chance. In the first case we speak of commensurability, or rationality. If everybody was rational, the common order would be easily attainable, so that all numbers were pictures by the points on the same line, and one could always find whether a particular quantity was great enough, or lacked something. Is that any different from natural numbers? Yes, it is, since we have to seek for a common measure every now and then, and the same thing will be called differently, depending on the unit system.
Perfect. Let everybody come to an accord and be happy. Unfortunately, not everybody can. There are all kinds of incommensurable, irrational... Just like in real life: they are much more plentiful than the rational elite! They are tremendously numerous, and this is not a mass to ignore. They form the very substance, the reality of the line, where rational numbers are so comfortable and spacious; that is why they are called real numbers. For each rational, there are more irrationals around than the quantity of rational numbers altogether. In any however tiny neighborhood. On the other hand, every real number can be gripped in a vice of rational numbers, as tightly as needed; this conveniently restores the complete linear ordering.
In the world of limited opportunities, there are no other completely ordered number systems. That is, any order at all brings the same image to the inner sight: a smooth line, which can easily be pictured as straight, provided we can close the eyes and leisurely glide along. This, too, has a name: continuity. Pits and bumps may break the spell sometimes; however, if they are not too many, the overall impression remains intact. After all, real numbers become a universal measure, with any distance expressible as a real number. Somewhere in infinity, beyond the borders of our world, there are other number-like things. For instance, the (ordinal) number ω (or rather ω0) that is greater than any other integer. The number ω1 is uncountably greater, and an infinity of (hyper)integer numbers can fit between the two. The overall order is thus extended onto infinite numbers; and for each infinity, there is the next, with no end. A serious person would not run after such intractable objectives; it is always commendable to keep in strict bounds and pursue a real purpose. That is, instead of idle promenades, better go straight from the point A to the point B. Or, in the numerical language, from zero to unity. Of all the real line, we are only interested in the segment [0, 1]. Thus we can be sure to reach the intended destination after a finite number of steps, for an arbitrary step size. To avoid racing through, just put a wall in the end. That is, we consider the segment [0, 1] together with its boundaries; some may wish to call it a closed manifold.
One is lucky to find that the number of points in the segment [0, 1] is no less than on the whole real line, and we do not miss anything. Rational number are also present here in full. How many? One cannot tell for sure; but this does not prevent us from naming. Let us denote the number of rational numbers with the term "aleph-zero" (À0), while the quantity of real numbers is associated with the word "continuum" (also known as "aleph-one", À1). There are all indications that the "cardinality" aleph-zero is strictly less than continuum. There are different opinions on whatever lying in-between; theoretically, we are free to fancy an entity like that, but nobody has managed to show up with anything palpable. Just console yourself with the well-established existence of quantities greater than continuum.
Indeed, imagine that every point of the segment [0, 1] is to be labeled with a number from the same range. Obviously, this is always possible, since the number of labels is exactly the same as the number of point to label. In this case, we say that there is a function form the segment (the "domain" of the function) into itself. In general, some points may bear the same label; such functions are not invertible, as one cannot unambiguously identify the prototype for any given function value. Well, nothing special, this is how life goes. Still, we can take all the namesakes together and declare that they constitute a kind of community, a subset of the segment [0, 1]. Now, the collection of all such subsets is found to be much vaster than the real axis; this means that the numbers of all bounded functions on the segment is greater than continuum. There are even greater cardinalities. But why? To start with, some vision of just one greater-than-real thing would be quite a deed.
As a first impulse, why not reproduce the trick with projecting the plane onto the real axis, just like we did to produce rational numbers? But look, thus "closing the fan" we got no increase of cardinality: the quantity of natural and rational numbers are the same (aleph-zero). Similarly, the number of points in a plane is the same as the number of points on the real axis (continuum). Still the basic line of though is quite acceptable; we only need to follow it a little farther.
One can easily imagine a square or a cube. The generalization to higher dimensionalities is rather straightforward. Many usual statements about our "domestic" space are directly applicable to abstract higher-dimensionality spaces. Yes, extrapolations may occasionally fail; the search for such catch-tricks (and striking teasers) has always been a well-gratifying mathematical amusement. With all that, there is an intuitive idea of a many-dimensional space, a kind of an abstract picture. We know that an ordered pair of points (at least close enough to each other) determines a spatial vector, which has both length and direction. Length is just a number, and we can naturally evoke the picture of a line. Imagination does not support higher-dimension angles; still, any two vectors lie in a plane, and the plane angle between them can be extracted from the scalar product. With a little more effort, one can picture all kinds of bodies, of three or more dimensions. Something floating inside a hypercube.
The axes of a many-dimensional space can be enumerated in some specific order. The transition from one enumeration to another does not change the overall geometry; still, some of its properties may be more tractable in a dedicated representation. The sequence of dimensions determines the orientation of the space. As the very possibility of axis enumeration implies an outer observer taking the space as a whole, it is not always possible to transform one geometric object into another by a continuous movement within the space, preserving the orientation of the both.
Now, let's look at the space of functions from the segment [0, 1] into itself. Admit that every point x of the segment corresponds to an axis of many-dimensional space; the value of the function in the point x is treated as the coordinate in this dimension. Then, every function can be geometrically represented as a point in the hypercube with a huge number of dimensions. Yes, their number is continuum. But this does not deny the spatial essence of a function, and we still have the geometry of plane and a 3-dimensional body, with the rest built on by analogy.
Note that physics has long since dealt with the spaces of infinite dimensionality. In quantum mechanics, state vectors may have infinitely many components, with a liberal mixture of the discrete and continuous spectrum, often adding some greater cardinalities. This does not prevent us from doing sensible calculations (though, possibly, not too rigorous from the mathematical standpoint). In fact, physical spaces are even cooler: there are also inner ("spinor") dimensions in each point! Here, let us keep on with a rather modest imaging.
A source of infinite amusement is to determine the classes of functions that correspond to the typical geometric objects, like point sets ("crystals"), curves, planes, bodies. For instance, the main diagonal of the hypercube pictures the family of functions that are constant on [0, 1]. It is obvious that all the subsets of the segment [0, 1] lie in the vertices of the hypercube. Indeed, every subset is associated with a characteristic function that takes only two values: 0 or 1. A continuum-sized sequence of zeros and unities, by construction, specifies one of the vertex points. In particular, with the "natural" orientation of the hypercube, when the sequence of axes coincides with the segment [0, 1], the empty set is logically found in the origin of the coordinate system; it is represented by the continuous sequence of zeros. The opposite (the most distant) vertex of the hypercube corresponds to the sequence of unities representing the whole segment. Similarly, some other families of functions can be visualized as many-dimensional entities embedded in the hypercube. This may suggest useful implications.
Geometry will only respond to its name, when we can measure something in a space. In the ordinary (Euclidean) spaces, this is achieved using a multidimensional version of the Pythagorean theorem. By analogy, one can define the norm of a function as the distance from the origin:
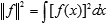
In the same manner, the distance between two functions is defined as the length of the difference vector:
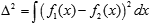
In particular, the distance between the opposite vertices of the hypercube equals 1, while the distance between any two «adjacent» vertices (forming a finite- or countable-dimensional hypercube) equals 0. This is naturally complemented with the notion of the angle between two functions:
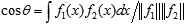
We do not need to precise the sense of integration in the above formulas. Each definition has a peculiar (and possibly useful) geometrical interpretation.
With this definition, certain thing look quite naturally. Thus, the norm of a constant function is trivially equal to its value. The distance between the functions f (x) = a and f (x) = b is |a – b|, while the cosine of the angle between them is always unity: as expected, such functions are parallel. The squared norms of the functions f (x) = x and f(x) = 1 – x are both equal to 1/3, as well as the distance between them; the cosine being estimated as 1/2, we get the angle of 60º. These two function represent the family of unitary transmutations on the segment [0, 1] (changing the orientation of the coordinate system). Clearly, such a tangled function can always be ordered by the function value and thus reduced to the same simple form f(x) = x ; consequently, the norm of any transmutation is also 1/3, while the mutual distances and angles may significantly differ.
This brings us back to the possible specifications of the integral. For one possibility, to compute the integral of any function, we first rearrange the dimensions of our hypercube to monotonically order the function values; after that, the integral is defined as the area under the resulting curve. Since only regular functions are involved, there are no serious technical intricacies, and any integral will evaluate in a number between 0 and 1. Of course, some precautions are still necessary. Thus, for a non-bijective (but otherwise smooth) function, the equal function values get to the "adjacent" points of the rearranged segment, and the corresponding measure (the elementary length dx) should be multiplied respectively. For an alternative picture, one might redefine the "density" of the points on the segment. However, this does not much hinder geometrical vision.
The characteristic functions of the subsets are, therewith, conveniently tractable. After rearrangement, every such function becomes a unit step function: zeros first, unity values to the end of the segment. The norm is then defined as the length of the unity part (which is exactly the number of elements in the set, its continuous measure). For example, the distance between two characteristic functions is determined as the measure of their union, minus the measure of the intersection.
Well, infinities are certain to have at least some crazy turns. For instance, the general formula evaluates the distance between the constant functions 0 and 1 (the opposite vertices of the hypercube) as 1. But everybody knows that length of the diagonal in the unit plane square equals 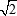 ! Here, it happens that the diagonal is unity, with all the edges of the same size. Quite a mystical thing. ! Here, it happens that the diagonal is unity, with all the edges of the same size. Quite a mystical thing.
At the second sight, it's no wonder. The purely Pythagorean diagonal of the N-dimensional unit cube equals 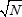 . With N → ∞, one obtains an intractable something of the . With N → ∞, one obtains an intractable something of the 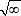 type. To normally work with such constructs, it is convenient to normalize all the lengths: in the finite-dimensional case, mere division by type. To normally work with such constructs, it is convenient to normalize all the lengths: in the finite-dimensional case, mere division by 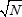 is enough; for continuum, we get a kind of density in the sequence of the spatial dimensions. In the same manner, one could normalize the usual two-dimensional square too, which is equivalent to the choice of a different unit for its diagonal, so that to make its length equal 1, just like in the infinite-dimensional space. This is a quite logical approach: in physics we often switch to some "natural" unit sets; similarly, relativity relates all the speeds to the speed of light, which corresponds to some experimentally observed symmetries. is enough; for continuum, we get a kind of density in the sequence of the spatial dimensions. In the same manner, one could normalize the usual two-dimensional square too, which is equivalent to the choice of a different unit for its diagonal, so that to make its length equal 1, just like in the infinite-dimensional space. This is a quite logical approach: in physics we often switch to some "natural" unit sets; similarly, relativity relates all the speeds to the speed of light, which corresponds to some experimentally observed symmetries.
There is a much more annoying problem. The integral definition of the norm is not unambiguous, since any integral is evaluated up to an arbitrary contribution of zero measure. That is, in fact, we do not determine the distance between individual functions, but rather between some classes of functions. Mathematicians would not much bother: their science is entirely like that. A man-in-the-street would prefer a nicer definition of distance to comply with the visible separation of spatial points. For instance, a circle (or a sphere) with the center in an inner point corresponds to all functions equally distanced from a fixed function. The variations of zero measure heavily spoil the picture, since they form an infinite class of functions, and the corresponding hypercube points are everywhere dense. What, then, is left of the geometrical obviousness? Things are even more aggravated, when it comes to the metrical definition of the vicinity, neighborhood, open and closed classes of functions etc. Any topological constructs are no longer simple and intuitive.
Yes, one can observe that the class of all functions can never be completely ordered and thus packed into the real axis. Its cardinality is higher than continuum, and that does it. One could practice severe self-restriction, considering very simple functions (say, diffeomorphic to a constant). In this case the hypercube closeness will coincide with metric proximity, and one will operate with trajectories, smooth transitions in the function space. However, many interesting functions will be left beyond that narrow scope, including permutations and characteristic functions. There is yet another approach: instead of the common space for everything, consider a layered space, a hierarchy of function classes, so that the usual metric is retained within each class, while any aggregate estimates are feasible on demand. For example, an arbitrary function can be represented with a (direct) sum of components: finite point set based subsystems, infinite discrete subsystems, and a number of continuous (or piecewise-continuous) areas. Instead of a single distance, we thus get three respective distances, one for each independent component (level). That is, instead of bluntly ignoring the regions of zero measure, we account for their contributions in a special way, treating them as singularities. In a different formulation, one could speak of singular measures (of the δ-function type). Provided the corresponding subspaces are orthogonal, the overall distance could be naturally defined by the sum of squared partial distances (normalized in a standard manner). One is free to suggest any other modes of aggregation, depending on the practical needs. In this way, the functional geometry won't become too cumbrous, leaving much room for graphical intuition.
May 1992
|