Абстрактные картинки
Наука математика (как и всякая наука вообще) сводит наши обыденные проблемы к формальностям. И это правильно. Потому что иначе приходилось бы заниматься только повторением пройденного, и на творческие задумки уже не хватало бы сил. Но пока человек отличается от пчелы, ему недостаточно знать, как действовать, — ему еще надо бы понять, как это выглядит в целом, со стороны, из другой вселенной... Это называется: интуиция. Когда оно есть — даже формальности становятся излишними, и дело движется вперед семимильными шагами.
Но люди разные. Интуиция одного может оказаться совершенно неприложима к другому. Кому-то вполне достаточно представлять себе последовательность действий — "дао", процессуальность как таковую. А всякие там картинки — это как результат. Другим подобная алгоритмичность претит: им, наоборот, что-нибудь нарисованное, чтобы со всех сторон посмотреть, а потом уже решать. Одни в музыке ловят мелодию — другим ближе гармония. Третий путь — инструментальная интуиция, практическое чутье, умение на лету выстроить, нарисовать, сыграть... Для этого и слово другое придумали: талант.
У математиков интуиция особого рода. Порядок у них выражается числом — а картинками заведует геометрия. Однако числа постепенно превращаются в абстрактные структуры, которые вполне возможно представлять себе геометрически; наоборот, геометрия растворяется в гомеоморфизмах и сводится к числовым (топологическим) инвариантам. И талант математика перерастает в логику, умение усматривать главное, абстрагироваться от мелочей.
По жизни, нам как раз мелочи интереснее всего. То, что можно постепенно разглядывать. Но сами по себе — мелочи превращаются в хаос, и это скучно. Поэтому важно прилепить их к какой-нибудь абстракции, чтобы чувствовать в зыбях твердость и не расстраиваться зря. Если же абстракция к тому же еще и наглядна — тут никакие бури не страшны, и занудный штиль можно перетерпеть.
Вот и давайте пофантазируем на тему визуализации чисел.
Числа, как известно, бывают разные — тут все как у людей. Начинается, натурально, с простого перечисления, подсчета. Раз, два, три, четыре, пять — дальше можно не считать. Почему? Да потому что уже есть общее представление о процессе. То есть, нарисовалась некое направление, вдоль которого мы равномерно шагаем.
Рациональные числа при таком раскладе нормально увидеть как парочку независимых направлений — и по каждому свои шаги. Возникает нечто вроде плоской решетки. Тут черт приносит какого-то работягу с дурацким вопросом: а что, если мы будем шагать разными шагами в одном и том же направлении? Сумеем прийти к чему-то общему или нет? Оказывается, все зависит от размера шагов. В каких-то случаях можно договориться, в других — ни в какую. Это называется соизмеримость. Или рациональность. Когда все рациональны — можно навести порядок, и снова все числа представляются точками на прямой, и всегда есть возможность сказать, чего больше, и чего не хватает. В чем отличие от натуральности? В том, что приходится каждый раз согласовывать наши мерки, и одно и то же называется по-разному, в зависимости от того, чем его измерять.
Прекрасно. Вот, мы договорились меж собой — и все довольны. Нет, не все. Остаются всякие там несоизмеримые, иррациональные... И прямо как в жизни: таких намного больше, чем пробившихся в рациональную элиту! Их так много, что игнорировать никак не получается. Именно они — основная масса, вещество той самой прямой, на которой рациональные размещаются просторно и с комфортом; потому и название: вещественные. Или действительные. На каждого рационального вещественных по соседству больше, чем всех рациональных вместе взятых. В любой, сколь угодно малой окрестности. С другой стороны, всякое вещественное число с обеих сторон можно сколь угодно плотно зажать между парочкой рациональных — и тем самым восстановить на вещественной прямой полный порядок.
В мире ограниченных возможностей никаких других полностью упорядоченных числовых систем больше нет. Любой порядок представим все той же картинкой: сплошная линия — которую всегда можно вообразить себе совершенно прямой, если закрыть глаза и плавно ехать вдоль. Для этого есть свое название: непрерывность. Колдобины и неуместные препятствия непрерывность нарушают — но если их немного, общее впечатление сохранится. В итоге вещественные числа становятся мерой всему, и любое расстояние можно выразить вещественным числом. Где-то там, за гранью нашего мира имеются и другие, бесконечные числа. Например, целое число ω (точнее, ω0), которое больше любого другого целого (а значит, и любого вещественного) числа. А за ним следует число ω1, и между ними бесконечность (гипер)целых (или гипердействительных) чисел, которые прекрасно упорядочиваются — но бесконечно велики. И так далее. Чтобы не бегать далеко и держать себя в рамках, у человека серьезного есть конкретная задача: движемся мы не просто так, а из точки A в точку B. Или в числовых обозначениях: от нуля до единицы. Из всей прямой нас в каждом конкретном случае интересует лишь отрезок [0, 1]. Тогда при любой длине шага мы таки дойдем до заявленной цели за конечное число шагов. А чтобы не проскочить — всегда можно поставить стенку в конце. То есть мы рассматриваем отрезок вместе с его границей; кому хочется, может называть это сегментом, или замкнутым многообразием.
Как выясняется, точек на отрезке [0, 1] ничуть не меньше, чем на всей числовой прямой — так что, ограничивая себя, мы ничего не потерям. Соответственно, и рациональных чисел там очень много. Сколько? Мы толком не знаем — но опять-таки, кто мешает придумать название? Пусть количество целых или рациональных чисел называется "алеф-нуль" (À0), а количество вещественных — обозначим словом "континуум". При этом есть все основания полагать, что "кардинальное число" алеф-нуль строго меньше, чем континуум (À1). Насчет того, что между ними — есть разные мнения; предположить существование чего-то такого мы можем, но добыть и пощупать пока не удалось. Зато мы точно знаем, что есть количества и побольше континуума!
Действительно, представим себе, что каждую точку отрезка [0, 1] мы хотим пометить каким-нибудь числом из того же диапазона. Понятно, что сделать это всегда возможно (поскольку количества точек в "области определения" и в "области значений" одинаковы). Тогда мы говорим, что на отрезке задана функция. Некоторые точки, в принципе, могут называться одинаково — такая функция будет необратимой: по имени мы не сможем указать, к чему имя относится. Дело, как говорится, житейское. Зато мы можем взять всех однофамильцев вместе и сказать, что они образуют некую общность — подмножество сегмента [0, 1]. Так вот, оказывается, что количество таких подмножеств намного больше количества вещественных чисел; соответственно, мощность множества всех ограниченных функций на отрезке больше мощности континуума. И можно придумать еще громаднее. Но зачем? Для начала нам бы представить себе, как выглядит нечто, не помещающееся на прямой...
Казалось бы, а почему не повторить трюк с размещением точек на плоскости в пределах вещественной оси? — как мы переходили от целых чисел к рациональным. Но вспомним: такое "свертывание веера" не увеличило полного количества точек. Мощности множества целых и рациональных чисел выражаются кардинальным числом алеф-нуль. Точно так же, вещественных точек на плоскости ровно столько же, сколько на вещественной прямой — континуум. Однако направление мысли достаточно разумное. Только надо пойти чуть-чуть дальше.
Мы легко можем представить себе квадрат и куб. Обобщение на большее число измерений мыслится как нечто в том же духе. И многие свойства привычного в быту пространства прямо переносятся на абстрактные пространства высших измерений. Разумеется, в каких-то случаях экстраполяции не срабатывают: поиск таких подковырок (а это прекрасная реклама!) — любимое занятие математиков. Но в целом у нас есть интуитивное представление о пространствах высокой размерности в виде некой абстрактной картинки. Мы знаем, что упорядоченная пара точек (по крайней мере, достаточно близко расположенных) задает вектор в пространстве, и у вектора есть длина и направление. Длина — это уже нечто одномерное, и обращаться с этим мы умеем. Многомерные углы воображение не отрабатывает — но два вектора всегда лежат в одной плоскости, и плоский угол между векторами определить легко по их скалярному произведению. Чуть больше воображения — и можно представлять себе всякие тела, в том числе многомерные. Плавает эдакое нечто внутри гиперкуба.
Измерения многомерного пространства можно упорядочить, перенумеровать. Переход к другой нумерации не меняет геометрии — однако описывать какие-то свойства в одном представлении может быть проще, чем в другом. Последовательность измерений называется ориентацией пространства. Поскольку же мы перечисляем измерения извне, наблюдая пространство в целом как бы со стороны, не всякие геометрические объекты одной размерности можно перевести друг в друга непрерывным образом с сохранением их собственной ориентации.
Теперь обратимся к пространству функций, переводящих отрезок [0, 1] в себя. Допустим, каждая точка отрезка соответствует измерению многомерного пространства, а результат вычисления функции в точке x — координата по соответствующему измерению. Тогда любую функцию можно геометрически представлять себе как точку гиперкуба с очень большим числом измерений. Да, их континуум. Но от количества измерений суть пространственности как таковой нисколько не страдает: у нас в распоряжении все те же геометрические образы плоскости и трехмерного тела, и все остальное — по аналогии.
Заметим, что в физике пространства сколь угодно большого числа измерений — далеко не новость. Вектора состояния в квантовой механике могут иметь бесконечно много компонент, свободно перемешивая дискретный и непрерывный спектр с чем-то вообще заоблачным. И никому это по жизни не мешает. На самом деле, там еще круче: есть внутренние, "спинорные", измерения. Но пока не будем замахиваться на такие высоты.
Можно долго и увлеченно забавляться выяснением, какие классы функций соответствуют различным геометрическим объектам: дискретным множествам ("кристаллам"), кривым, плоскостям, телам. Например, главная диагональ гиперкуба задает семейство постоянных функций на отрезке [0, 1]. Сразу ясно, что все подмножества отрезка [0, 1] расположены в вершинах гиперкуба. Действительно, каждое подмножество задано соответствующей характеристической функцией, принимающей только два значения: либо 0, либо 1. А последовательность нулей и единиц длины континуум как раз и задает одну из вершин. В частности, при "естественной" ориентации гиперпространства, когда последовательность координат совпадает с отрезком [0, 1], пустое множество логично попадает в начало координат: это последовательность из одних нулей. Противоположная ему (самая удаленная) вершина — соответствует континууму единиц, представляющему отрезок целиком. Точно так же, любые другие семейства родственных функций можно увидеть внутри гиперкуба. И делать из этого интуитивные выводы.
Геометрия становится собственно геометрией, когда в пространстве можно что-то измерить. В обычных (евклидовых) пространствах работает многомерный вариант теоремы Пифагора. Можно по аналогии говорить о норме функции как расстоянии от начала координат:
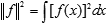
Соответственно, расстояние между функциями определяется как длина вектора-разности:
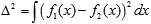
В частности, расстояние между противоположными вершинами гиперкуба равно 1, а расстояние между любыми "соседними" вершинами (образующими конечномерный гиперкуб) равно 0. Это естественно дополняется понятием угла между функциями:
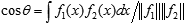
В каком смысле определены эти интегралы — мы пока уточнять не будем. Для каждого определения есть своя геометрическая интерпретация.
Некоторые вещи в таком определении выглядят очень естественно. Например, норма постоянной функции просто равняется ее значению. Расстояние между функциями f (x) = a и f (x) = b равно |a – b|, а косинус угла между ними всегда равен единице: вполне ожидаемая параллельность. Квадраты нормы для функций f (x) = x и f(x) = 1 – x одинаковы и равны 1/3; расстояние между ними равно той же величине, а косинус угла равен 1/2 (угол в 60º). Эти две функции принадлежат классу унитарных перестановок на отрезке [0, 1] (изменение ориентации системы координат). Понятно, что такую "перепутанную" функцию всегда можно упорядочить по значению и тем самым вернуть к виду f (x) = x ; следовательно, норма любой перестановки равна 1/3 — при значительном разбросе взаимных расстояний и углов.
Это возвращает нас к вопросу об определении интегралов. Чтобы вычислить интеграл для произвольной функции, мы сначала упорядочиваем функцию по значению — и потом вычисляем площадь под полученной кривой. Поскольку речь идет об ограниченных функциях, дополнительных технических проблем тут не возникает: любой интеграл оказывается числом от 0 до 1. Разумеется, есть свои маленькие хитрости. Например, если непрерывная функция не является взаимно-однозначной, одинаковые значения попадают в "соседние" точки отрезка, и соответствующую меру (длина элементарного интервала dx) придется удваивать, утраивать и т. д. Эквивалентное представление: изменяется "плотность" размещения точек на отрезке. Но это не разрушает геометричности как таковой.
Теперь понятно, как работать с характеристическими функциями подмножеств. После переупорядочения такая функция превращается в "ступеньку": сначала нули, потом единицы. Норма функции определяется как длина отрезка с единицами — а это есть в точности количество элементов подмножества (его мера). Расстояние между характеристическими функциями есть мера их объединения за вычетом меры пересечения.
Разумеется, у бесконечностей свои капризы. Например, расстояние между постоянными функциями 0 и 1 (противоположные вершины гиперкуба) по общей формуле равняется 1. Но мы же знаем, что диагональ единичного квадрата имеет длину 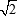 ! А здесь получается, что все стороны равны 1, а диагональ тоже единица! Чудеса. ! А здесь получается, что все стороны равны 1, а диагональ тоже единица! Чудеса.
На самом деле все в норме. По-пифагоровски, диагональ N-мерного единичного куба равна 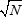 . При N → ∞ мы получили бы непонятность вида . При N → ∞ мы получили бы непонятность вида 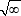 . Чтобы нормально работать с такими конструкциями, можно все длины нормировать: в конечномерном случае делить на . Чтобы нормально работать с такими конструкциями, можно все длины нормировать: в конечномерном случае делить на 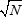 — а в непрерывном случае это превращается в плотность последовательности измерений пространства. Разумеется можно было бы нормировать и двумерный квадрат: для его диагонали мы просто выбираем другую единицу измерения, и в этих новых единицах длина диагонали равна 1, в полном соответствии с бесконечномерным случаем. Решение достаточно логичное: в физике мы таким образом выбираем "естественные" единицы — или, например, привязываем все скорости к скорости света, и это удобно для описания наблюдаемых симметрий. — а в непрерывном случае это превращается в плотность последовательности измерений пространства. Разумеется можно было бы нормировать и двумерный квадрат: для его диагонали мы просто выбираем другую единицу измерения, и в этих новых единицах длина диагонали равна 1, в полном соответствии с бесконечномерным случаем. Решение достаточно логичное: в физике мы таким образом выбираем "естественные" единицы — или, например, привязываем все скорости к скорости света, и это удобно для описания наблюдаемых симметрий.
Куда более существенная проблема — неоднозначность норм, которые определены лишь с точностью до множества меры нуль (интеграл по которому равен нулю). То есть, мы определяем расстояние между семействами функций, а не между конкретными функциями. Для математиков это в порядке вещей: у них всегда так. Человеку простому хотелось бы иметь такое определение расстояния, которое интуитивно соответствовало бы визуальному разделению пространственных точек. Например, окружность (или сфера) с центром во внутренней точке — функции, равноудаленные от некоторой заданной функции. Но отличия меры нуль определяют бесконечное семейство функций, и соответствующие точки всюду плотно распределены по гиперкубу. Как-то не вяжется с геометрической наглядностью. Особенно, если использовать метрику для определения понятий окрестности, открытых и замкнутых классов функций и т. д. Любые топологические построения становятся отнюдь не интуитивными.
Конечно, можно заметить, что класс функций ни при каком раскладе невозможно сделать полностью упорядоченным, впихнуть в действительную ось. На то она и кардинальность выше континуума. Можно пойти по пути самоограничения и рассматривать только функции достаточно простого вида (например, диффеоморфные постоянной). Тогда близость в гиперкубе совпадет с метрической близостью. И можно рассматривать траектории в пространстве функций, и плавно переходить от одного к другому... Однако многие интересные функции окажутся тогда за бортом. В частности, перестановки и характеристические функции подмножеств. Но есть еще вариант: вместо одного пространства на всех — расслоенное пространство, иерархия классов функций, внутри каждого из которых расстояние будет геометрически определенным, а все вместе можно при необходимости агрегировать в нечто общее. Например, произвольная функция представляется (прямой) суммой компонент: подсистемы конечного множества точек, бесконечные дискретные подсистемы, компоненты мощности континуум (кусочно-связные области). Соответственно, вместо одного — получаем три расстояния, или больше — по числу компонент (уровней). То есть, вместо тупого игнорирования вкладов от множеств меры нуль, мы учитываем их особым образом, как особенности. В другой формулировке — речь идет о сингулярных мерах (типа δ-функции). Поскольку соответствующие подпространства ортогональны, естественно определить общее расстояние через сумму квадратов (нормированных) расстояний по отдельным компонентам. Или еще как-нибудь. Геометрия будет ненамного сложнее — а для интуиции простор.
май 1992
|