Perceptive Forms
The abstract mathematical space indifferent to anything that might happen inside it is one of the greatest achievements of the human mind demonstrating our ability to break free from the barriers of our inherent finality and aim at comprehending of the world as a whole, with the side effect of clarifying the humanity's place in all that immensity. Still, as long as we need to take care of our local affairs, there is no disgrace in accounting for what and where we are, to sensibly weigh our real capacities and never pretend to anything beyond the reasonable; otherwise, what's the use of our reason? Within this limited universe, one surprisingly finds that bare mathematical space is not always the best idea we might have about the reality around us, and that the formal simplicity has to be augmented to an ugly ad hoc construction, to be practically tractable and feasible. Such a tailor art may gradually transform into a common habit and everyday routine, with this abstract formality being quite fit for becoming yet another mathematical theory, which, in its turn, cannot be satisfactory in all respects and demands an informal extension. That's right, life never stays the same, and our science has to keep pace with cultural development.
The principal difference of the perceptible world from an abstract mathematical concept is in that nobody ever gives us a ready-made space in all its entirety: we have to repeatedly reconstruct our space adjusting it to the current activity. Of course, nobody starts from scratch: there are numerous templates and half-products, so that one can always find something of the kind and combine a preliminary picture of the new spatiality from the already known building blocks. This original metaphorical models will later accumulate a lot of corrections and specifications, to become a powerful operating tools; in a little while, people will manage to derive all that eclectic appearance from a general idea, thus adding yet another universal technology to the stock.
For an illustration, let us slightly spice up our vision of the trivial everyday space. Since the beginning of time, we treat it as three-dimensional. The three dimensions are basically equivalent for mathematics, while humans not only find them qualitatively distinct, but also stress the difference with a choice of names, varying from typical situation to another: "length—width—height", "length— width—depth", "width—height—depth", "distance—azimuth—declination", and so on. When it comes to placing one thing inside another, two parallel parameter kits are considered, with the appropriate selection of the names. Human perception is never passive, it represents the outer world in terms of human activity. To look at a thing to the left or to the right of us, we need to turn to the corresponding direction by an appropriate angle; to evaluate height, we need at least to tilt the body, or maybe go up/down; to measure distances, we need a quite different instrumentation, selecting between varieties each suited to a particular spatial range; as for the depth, we often cannot immediately grasp it at all, which leads to a wide usage of indirect methods (the same holds for the objects beyond the perceptive horizon).
A formal model of the perceptive space will necessarily differ from a model of the space "as it is". Admit that some finite-sized thing is placed at some distance r from the observer. This phrase already involves a very strong abstraction: since, in general, the distinct parts of the thing imply the distances of their own, we need to both take the thing as a whole (which refers to some average, or integral, distance from the observer) and consider its spatial organization, with a number of well-discernible details that can be inspected one by one (at least, to produce an impression of integrity, to present the object to our senses so that we could recognize it as that particular thing). The activity of observation will therefore unfold itself into a series of observation acts, each presenting us a part of the whole, namely, the one appearing in the currently formed "focus of attention". This zone of immediate grasp cannot, of course, be reduced to a single point; sometimes it covers a spatial zone vast enough to absorb the whole object, which, in this case, is perceived as a "point"; still, most often, one has to move the focus of attention within some global "field of vision" in the attempt to find the edges of the object (or some other border features). As a result, the object gets represented by the structure of the process of examination. In real life, one rarely sticks to a single file of fixation points: the total time of observation normally allows tracing many virtual paths and thus, to certain extent, get free of the superficial impressions to come to a relatively stable and more consistent vision of the thing.
To make it clearer, let the observer's look stroll in just two dimensions; a segment of a straight line with the center at the distance r from the eyes will do as an object to observe; let it lie in the horizontal plane and be orthogonal to the (shortest) line of sight. Then any single act of observation means slightly turning the head to the left or to the right within the same plane. In every such act, at each angle of sight, the focus of attention covers the points of the object segment that do not much deviate from the line of sight (let this spread be characterized by a small angle ε). For the observer, all such points form a segment of line with the length l; for the direct look, this coincides with the range of point within the segment to observe: Δx = l. Always assuming the validity of the laws of the linear optics, one could draw the picture of observation as follows:
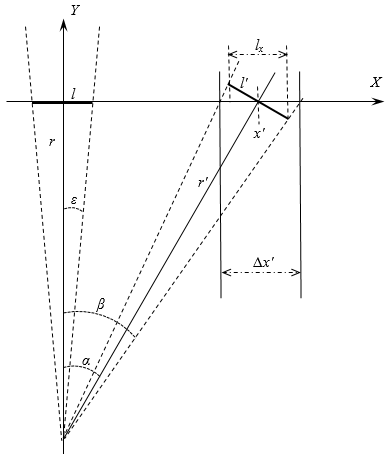
Certainly, to get a non-zero angle of sight one has to account for both the optical form of the eye and binocular vision; the latter is also important in estimating the distance to the object. However, such physiological considerations have nothing to do with perception as such, since it is a kind of activity, that is, a phenomenon of a higher level, compared to any biology. The bodily organization of perception may largely vary, up to elimination of any organic components at all.
When the line of sight gets tilted by the angle α the focus of attention moves to the point x', thus presenting a new fragment Δx' of the object to the observer, who perceives it as a segment with the length l' orthogonal to the line of sight, at a somewhat greater distance r'. Since we are to keep within the original straight line, the sight cannot be deflected too much, and 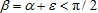 . Obviously, . Obviously,
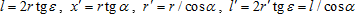 . .
That is, with greater α, we can grasp a longer segment of the object line at once:
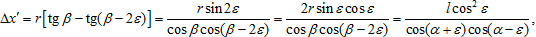
so that, at 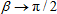 , ,
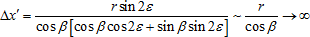
Nevertheless, the projection of l' onto the axis X has the same length for any direction of sight: 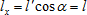 . This roughly describes how the fine details of the picture get lost far from its center: any discrete structure gets eventually absorbed by the focus zone, producing the impression of continuity. . This roughly describes how the fine details of the picture get lost far from its center: any discrete structure gets eventually absorbed by the focus zone, producing the impression of continuity.
Inside the focus zone, we neglect the difference in the distances of the point of the object line X from the observer: they all belong to the same level of hierarchy. That is why we can model the focus zone by a segment orthogonal to the line of sight. However, the alternative representation with a small arc does not introduce any significant corrections, and the visible size of the focus zone, as the correction
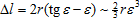
is an infinitesimal of a greater order at small ε (that is, it belongs to a different level of elaboration). The issue of the primacy of the straight line or the arc (sliding movement vs. rotation) may be of high importance, say, for the foundations of physics; but here, we talk about something else.
In general, one can focus on an arbitrary point of the object line. The perceptive form will then be represented by a continuum of fragments of different size. For a complete description, a finite number of observation acts is enough, as soon as their respective zones cover the entire span of the object. Every such map reveals a hierarchical structure, arranging the parts of the object by their distance from the observer. There are as much covers like that as you like; still, all of them belong to the same integrity, representing the object as a whole. Such an integrity that can unfold itself into various (though never arbitrary) hierarchical structures is called a hierarchy. Perception as an activity is hierarchically organized.
We have demonstrated, how a very primitive mathematical model could lead to the idea of hierarchically structured "inner" space used by the subject to regulate any other activity. More realistic models would account for the "fine structure" of the perceptive act, as general psychology indicates that any action within an activity grows into a hierarchy of operations; for instance, the zone of immediate grasp might be represented by an angular (say, Gaussian) distribution rather than a mere range of angles. In this case the overlap of the zones is to produce an analog of a musical timbre, with the angle of 2ε playing the role of the principal tone. Such an underlying structure implies certain considerations of regularity and stability (robustness) of such "inner timbres": there are those that are better fit for zone discrimination and emergence of a well-defined scale. As we know, in music, a similar approach predicts just a few preferable pitch scales (associated with the base collections of tones, musical modes, or chords); there are only two scales that can pretend to universal significance and recognizably reproduce any musical intonation at all. The same structure has also been empirically discovered in visual arts; however, without any sound reasons for such an eminent resemblance.
To be precise, there is no need to cover all the object with the focus zones; instead of a complete map, one could just take a few reference directions, with all the rest somehow "interpolated". Putting aside any big science, one can easily comprehend that by personal experience. People are apt to judge by a couple (or so) of "typical" traits, never bothering about too thorough investigation. The standard techniques of producing a plot of a function follows the same line: first, we ponder a little over the selection of reference points, then we connect the images of the selected points with a smooth line (a kind of spline). Of course, the quality of the graph will depend on the choice, and on our ability to detect the singularities; in our everyday experience, we sometimes make errors, but life will quickly put things in their proper order.
For one of the most important corollaries of the zone model of perception, one could mention the inner hierarchy of each scale, the presence of "embedded" discrete substructures. In the simplest model, we could arbitrarily change the distance from the object, obtaining different perceptive hierarchies (the collections of maps with varying zoom factor). In a more realistic approach, like the above inner timbre model, the feasible scales are not arbitrary, and we get a number of preferable observation points depending on the nature of each scale.
Earlier, considering the "grazing look" limit 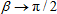 , we, of course, violated the model's applicability conditions. In reality, the possible range of observation angles (the observation field) is determined by the character of activity; it will never be too extended. When the number of focus zones to cover the object is too high, this hints to the necessity of moving to a different level of hierarchy. That is, we feel ourselves as if we were inside the object, which results in a split view presenting the whole object as a collection of distinct parts, which can be viewed using the standard active inspection technique. In the opposite limit, with the object entirely covered by a single zone, leads us to the notion of a point, which too requires switching the level: there are no points in real life, and the inability of discern anything means that we just overlook something that could be revealed at a closer examination. , we, of course, violated the model's applicability conditions. In reality, the possible range of observation angles (the observation field) is determined by the character of activity; it will never be too extended. When the number of focus zones to cover the object is too high, this hints to the necessity of moving to a different level of hierarchy. That is, we feel ourselves as if we were inside the object, which results in a split view presenting the whole object as a collection of distinct parts, which can be viewed using the standard active inspection technique. In the opposite limit, with the object entirely covered by a single zone, leads us to the notion of a point, which too requires switching the level: there are no points in real life, and the inability of discern anything means that we just overlook something that could be revealed at a closer examination.
The mathematics of zone perception pictures it as a process unfolding in some global (embedding) space, so that any perception theory could be developed in respect to that formal space. Now, let us put the logic upside down: one might conjecture that the hierarchical vision of space reflects its true nature, while any abstract absolutes only refer to a specific level of hierarchy, a range of prototype activities. Such a position may superficially seem a regression to the primitive anthropocentric view of the world that was so hard to get rid of in the history of science (and some science is still too anthropomorphic to be true). Admitting that the form of an object could depend on the way of viewing looks like stuffing the theory with unworldly subjectivity, mystics and voluntarism. But does anything in this approach specifically refer to the subject? We rather discuss the overall organization of the system, hierarchical structures. Any natural things interact on many levels, and the appearance of one thing for another depends on the nature of interaction, which does not need to be related to conscious activity: any physical phenomenon, or biological metabolism, will do as well. Let a robot view the same object instead of a conscious person; the machine will reconstruct the same image, as soon as the viewing technology is hierarchically structured. An electron will be a hierarchy for another electron, provided the act of interaction admits inner structure and gradual development. In physics, theoreticians often employ a kind of smooth introduction or removal of interaction ("turning on and off"). However, they usually take it for an auxiliary idea, a technical trick, making their best to remove any scaling parameters from the final result. Don't they suppress the physical sense (the purpose, the object area) of the theory that way? Abstract theories are deemed to describe anything at all; this is the principal source of formal and logical contradictions. Just take the relativity theory: first, we limit the propagation speed of any physical interactions, and right away, treat space-time as global and ready-made; isn't it crooked? To be consistent, we need to consider the process of reference frame formation, without too precocious assumptions about what will happen in the vicinity of the horizon (see the above note on the grazing-look limit), or beyond it. Well, such a theory would not show off spectacular singularities to collect easy funding. Instead, it would be a science about nature, and not about an abstraction that we pretend to pose as nature. The hierarchical approach, therefore, is to overcome the anthropocentric prejudice in a most drastic manner, while the formalistic (objectless) science tends to fall into all-embracing subjectivism. In the zone hierarchy vision, the existence of an embedding space means a fixed scale as a specific level of perception. For each scale, there is a objective hierarchy of embedded scales; with the transition to another scale, the whole construction will change, up to an unrecognizable figure of the same object. As long as we stay within a definite level, we are bound to get numerous "illusions" and "artefacts"; still, even those are not arbitrary, since they grow from the organization of that particular scale and hence are quite real in the course of the corresponding activity. Logically, this does not mean that we can identify such "inertial forces" with real, "physical" phenomena; nevertheless, in any activity, we have to account for our place in the Universe and act in accordance with our (albeit biased) vision of the world.
And now, the blunt question: does that have anything to do with math?
Yes, it does. The attempts of some mathematicians to oppose their science the rest of the human culture, to put themselves "above" nature and dictate their "absolute" truths to it, are of the same train as the attempts of the "deepest" physics to speak of the world in general rather than the small part we happen to face so far. Once having chosen a very special mode of perception, one tends to forget about all the other possibilities, the multifaceted nature that can be treated in many different (and not always compatible) ways. Within the limits of its applicability, such a castrated science is quite efficient and useful; as soon as it comes to assimilating complementary views, it becomes a handicap. Of course, no formality can stop life: it will penetrate mathematics through the heaps of concealment and vague assumptions, which are not to be exposed by the "rigorous" science to the wide public. Later on, somebody promotes a new paradigm, showing the bulk of the former theories in a brighter light, which allows to "naturally" unify them into a flash of beauty. A storm of applause and loud cheers: great! Presumably, that genius did not do anything special; it's mainly a matter of recollection of what the others have long since preferred to forget.
|