Логические симметрии и комплексная логика

Традиционно алгебраические представления в математической логике приписывают логическому значению истина число 1, а логическому значению ложь — число 0. При этом конъюнкция (Ù) и дизъюнкция (Ú) естественно соотносятся с алгебраическим умножением и сложением соответственно. Конечно, такая алгебраическая структура отличается от обычной арифметики, но сама возможность оперировать с числами вместо особых логических значений позволяет прояснить некоторые аспекты формальной логики и подсказывает варианты ее обобщения.

Но есть и другой подход, который также может быть в чем-то полезен при построении обобщенных логик. Вместо того, чтобы представлять логическое значение ложь нулем, мы можем сопоставить ему число –1. Обозначая логическое отрицание знаком минус, мы логично получаем, что –1 (ложь) — это не истина, а –(–1) равняется 1 по определению:

,

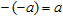где буквами a, b, c, ... мы обозначаем все, что может принимать логические значения: константы, переменные, логические выражения (формулы), содержащие константы, переменные и другие формулы в разных комбинациях; кроме того, можно рассматривать также логические функции как сокращения для каких-то выражений, а потом перейти к переменным функциям и функциональным выражениям... В нашем контексте такая иерархичность не существенна.

Введем теперь алгебраическое умножение * так, чтобы 1 * 1 = 1 and (–1) * (–1) = 1, с естественным выбором: (–1) * 1 = 1 * (–1) = –1. Эта операция, очевидно, соответствует логической эквивалентности; она коммутативна и ассоциативна:

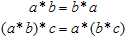
но, в отличие от конъюнкции и дизъюнкции, она не идемпотентна:

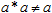
что, впрочем, не вызывает особого беспокойства, поскольку обычное числовое умножение тоже идемпотентностью не страдает. Отметим также, что

,

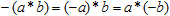в приятном соответствии с нашими арифметическими ожиданиями.

Введенное таким образом умножение симметрично в пространстве значений истинности: замена 1 ↔ (–1) приводит к той же самой таблице истинности для логической эквивалентности.

Подчеркнем, что знак равенства в этих и последующих формулах, обладая всеми свойствами эквивалентности, принадлежит логике нашего рассуждения (уровню методологии), а не логике его предмета. Алгебраические структуры этих уровней могут различаться, вплоть до способов введения логических значений. Равенство и неравенство могут использоваться только для сравнения формул предметной логики — но не внутри этих формул.

С учетом наших определений, мы можем формально исключить отрицание из теории, заменив его умножением:

.

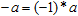Это открывает многообещающее направление исследований, поскольку мы устраняем весьма скользкие концептуальные моменты, вызывавшие бурные дискуссии на протяжении многих веков. С другой стороны, необходимость введения логического отрицания не очевидна в многозначных и нечетких логиках; все, на что мы может здесь сослаться, — это старинная традиция. Тем не менее, этот подход не решает проблему до конца: одно из логических значений почему-то оказывается предпочтительнее другого — а это, по сути дела, протаскивает в логику отрицание неявным образом. В качестве альтернативы можно было бы независимым образом определить неэквивалентность:

,

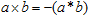что как бы вводит "дополнительное отрицание":

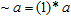
так что в итоге мы имеем полностью уравновешенную теорию, не требующую одноместных операций. Возможные приложения такой логики подчеркивают, что в реальной жизни установление эквивалентности и поиск различий — это очень разные (противоположные) деятельности, а между ними — море промежуточных вариантов.

Очевидно, значения истинности в нашей симметризованной логике могут быть выражены через две фундаментальные операции:

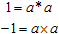
для любого a. Однако, поскольку эти определения неявно содержат квантор, они принадлежат более высокому уровню иерархии, и мы не имеем права вставлять так определенные логические значения в алгебру логики, если не принять специальных мер для уравновешивания теории, как в примере с двумя отрицаниями. Иначе говоря, пространство истинности глобально по отношению к предметной области: в принципе, могут быть и другие значения истинности, но каждое из них представляет предметный уровень целиком. Однако если речь идет о некоторых частных утверждениях относительно предметной области, допустимо использовать такие определения логических констант — сознавая, что полученные формулы относятся только к обычной двузначной логике.

Полностью симметричная логика может быть дополнена несимметричными операциями, которые зависят от структуры пространства истинности. Меняя местами истину и ложь, мы получим иные таблицы истинности для таких операций. Самые известные из таких операций — конъюнкция и дизъюнкция, которые связана друг с другом через отрицание:

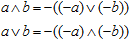
По отношению к определенным двум видам логического умножения, конъюнкция и дизъюнкция могут быть охарактеризованы как "аддитивные". В логике без отрицания они становятся независимыми, подобно независимо введенным эквивалентности и неэквивалентности. Но в двузначной логике (скрыто предполагающей отрицание) мы можем симметричным образом задать их взаимозависимость выражениями вроде

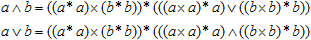
Аддитивные (несимметричные) операции могут показаться более фундаментальными по сравнению с эквивалентностью и неэквивалентностью, поскольку, вроде бы, несимметричные операции всегда можно скомпоновать симметричным образом, а наоборот — не получится:

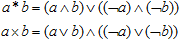
Формализм двузначной логики может, поэтому, быть построен, исходя из отрицания и одной-единственной несимметричной ("аддитивной") операции. Но эта простота обманчива, она целиком зависит от идеи логического отрицания — что, по сути дела, компенсирует одну несимметричность другой. В каких-то случаях ограничиваться такой, урезанной логикой было бы неправильно.

Исследуя возможность обобщений, полезно обратиться к Arithmetices Principia Пеано. Не придираясь пока к искусственности его теоретико-множественных формулировок, подчеркнем крайне важный момент: натуральные числа (по Пеано) начинаются с выбора единицы, а все остальные натуральные числа представляют собой определенной количество единиц. Современные математики склонны добавлять к натуральным числам еще и псевдо-число 0; это нарушает прозрачность и последовательность теории. Исходно, Пеано включает в свой список аксиом свойства числового равенства; последующие авторы исключают эти аксиомы на том основании, что они, дескать, следуют из логики — тем самым перепутываются совершенно разные вещи, разные уровни иерархии, а это недопустимо, при всем кажущемся "изоморфизме". Арифметика натуральных чисел выводится из единицы и единственной одноместной операции, инкремента (который было бы преждевременно трактовать как сложение с единицей). Однако такая индуктивная конструкция не позволяет сразу увидеть внутренние симметрии теории — поэтому вводят двуместные операции сложения и умножения, с формальным продолжением в виде вычитания и деления — которые уже не очень вяжутся с натуральностью. Вычитание неизбежно приводит к идее отрицательных чисел — и вводит ноль как число. Деление ведет к арифметике рациональных чисел, предпосылке вещественных чисел. Такое же развитие возможно и в алгебраически переформулированной логике. Однако здесь мы обратимся к другому возможному расширению — комплекснозначной логике.

Вспомним, что пространство логических значений устроено так, что (–1) * (–1) = 1. Можно попробовать похожим образом ввести логическое значение, представляющее собой "квадратный корень" из логического значения ложь: i * i = –1. Да, мы не знаем, что это такое, и как это изготовить из подручных средств. Но мы можем просто постулировать его существование и обозначить буквой i. Допустимость подобных концептуализаций давно уже стала краеугольным камнем современной математики. И все же в нашей алгебраической логике эта мнимая единица допускает вполне очевидную интерпретацию. Действительно, равенство a * a = 1 означает, что всякая логическая величина эквивалентна сама себе, — то есть, что a ≡ a есть истина (напомним, что здесь имеется в виду эквивалентность в предметной области, а не логика нашего описания). Тогда равенство i * i = –1 вводит в рассмотрение величину, которая не тождественна себе самой. Какой бы странной не казалась эта идея рационально мыслящему человеку, она отнюдь не нова, ее давно уже обсуждает философия (прежде всего гегелевская и марксизм). Таким образом, наша алгебраическая формулировка логики с комплексными значениями истинности может стать подходящим исходным пунктом для примирения научной и философской методологии.

В этой расширенной логике значения истинности могут иметь как вещественную, так и мнимую части. В зависимости от выбора "аддитивных" операций, мы получим разные правила манипулирования комплексными значениями истинности. В общем случае эти правила будут гораздо сложнее обычной комплексной арифметики. Это не отменяет соответствие как таковое. В частности, традиционная интерпретация фазы как угла поворота вектора в комплексной плоскости сразу же сопоставимо с интерпретацией логического отрицания как обращения вектора. Тут же появляется возможность различить повороты и зеркальные отражения — с тонкими различиями в логике.

Присутствие "фазовых" компонент в логических величинах открывает новые горизонты для квантовой логики, поскольку "наблюдаемая" рациональность связана с вещественными числами, а внутренние, зависящие от фазы компоненты мышления остаются в тени. Учет таких скрытых логических состояний вполне аналогичен переходу в механике от положения и импульса классической частицы к виртуальному движению во внутреннем конфигурационном пространстве, которое несопоставимо напрямую с наблюдаемыми величинами.

Подведем итоги. Симметризованная алгебраическая формулировка математической логики достаточно привлекательна, чтобы заняться исследованием ее возможных обобщений, включая многозначные, рациональные, нечеткие и комплексные логики. Особенно обнадеживает, что, с одной стороны, эта математика не требует революционных изменений и новых парадигм, а с другой, новые понятия остаются интуитивно ясными и доступными даже тем, кто не одобряет нагромождения формалистических хитросплетений. Иерархии логики еще хватает направлений нетривиального развития.

ноябрь 2003