ЗВУКОРЯДЫ: ЛОГИКА ВОСПРИЯТИЯ
П. Б. Иванов
1991
ОЩУЩЕНИЕ ЗВУКА И КОМБИНАТОРИКА ЧАСТОТ
Как человек слышит музыку? Первое интуитивное представление: ухо — приемник звука, мозг выделяет какие-то стороны звукового сигнала, составляющие собственно музыкальные впечатления. Следовательно, акустические основы музыки следует искать в самом внешнем звучании, они объективны, а развитие музыкального языка связано с расширением набора выделяемых из акустического сигнала характеристик.
Таков наиболее распространенный подход к построению теории музыкальных структур. В частности, попытки в его рамках объяснить возникновение звукоряда — устойчивого дискретного набора ступеней, из которого выбираются возможные высоты музыкальных звуков, — начиная с Пифагора, манипулируют частотами тонов, в их отношениях усматривая критерии музыкальности. Известно, что наиболее слитно звучат тона, частоты которых либо одинаковы (унисон), либо находятся в отношении 2 : 1 (октава) или 3 : 2 (квинта). В традиционной теории музыки эти интервалы называются совершенными консонансами. Менее слитно звучат несовершенные консонансы: кварта (отношение 4 : 3), большая терция (отношение 5 : 4) и малая терция (отношение 6 : 5). Кварта называется обращением квинты, потому что в сумме эти интервалы дают октаву: (4 : 3) ∙ (3 : 2) = (4 : 2) = (2 : 1). Заметим, что сложению интервалов отвечает умножение соответствующих отношений частот — такая шкала называется логарифмической. Обращением (дополнением до октавы) большой терции является малая секста (отношение 8 : 5), а обращение малой терции — большая секста (отношение 5 : 3), которая тоже считается несовершенным консонансом. Все остальные интервалы называются диссонансами. Таким образом, критерием "гармоничности" звучания становится требование, чтобы частоты звуков соотносились как небольшие (до 6) целые числа. Можно построить набор упорядоченных по величине интервалов, определяемых отношениями целых чисел:
| 2 : 1 | → | 0.000 | унисон |
| 16 : 15 | → | 0.093 | малая секунда |
| 9 : 8 | → | 0.170 | большая секунда |
| 6 : 5 | → | 0.263 | малая терция |
| 5 : 4 | → | 0.322 | большая терция |
| 4 : 3 | → | 0.415 | кварта |
| 3 : 2 | → | 0.585 | квинта |
| 8 : 5 | → | 0.678 | малая секста |
| 5 : 3 | → | 0.737 | большая секста |
| 7 : 4 | → | 0.807 | "чистая" септима |
| 16 : 9 | → | 0.830 | малая септима
(обращение б. секунды) |
| 15 : 8 | → | 0.907 | большая септима
(обращение малой секунды) |
| 2 : 1 | → | 1.000 | октава |
Отношения частот разнесены "по уровням гармоничности": левее всех совершенные консонансы, потом несовершенные, далее диссонансы. Дополнительно приведены величины интервалов как логарифмы отношений частот по основанию 2. Сложение (вычитание) интервалов отвечает при этом сложению (вычитанию) их величин; обращение интервала есть просто вычитание его величины из единицы. Гораздо удобнее сравнивать интервалы по их величине, чем по отношениям частот.
Построенные таким образом интервалы называются натуральными. Откладывание их от какого-либо фиксированного тона дает набор звуков, называемый натуральным звукорядом. Разумеется, здесь приведены не все возможные отношения, так что между любыми двумя ступенями натурального звукоряда существует другая ступень — и натуральный звукоряд содержит бесконечное количество звуков! Ясно, что практическое использование бесконечного звукоряда невозможно, — и теоретики потратили немало усилий, чтобы как-то отсеять все "лишнее" и объяснить, почему одни интервалы можно употреблять в музыке, а другие нельзя. В частности, еще в XVIII веке обратили внимание на сложный состав музыкальных звуков: кроме основного тона с частотой f в состав любого звука входят обертоны с частотами 2f, 3f, 4f и т. д. Таким образом, каждый звук как бы содержит в себе натуральный звукоряд! Однако человек ощущает лишь ограниченный диапазон звуковых частот. Следовательно, ряд гармоник (обертонов) любого звука где-то обрывается, и натуральный звукоряд становится конечным. Из оставшихся звуков пригодны к употреблению в музыке лишь те, основные тона которых, при совместном звучании, не вызывают неприятных биений. Биения между обертонами как правило значительно слабее; их наличием определяется "степень совершенности" консонанса.
Такова, в общих чертах, психофизиологическая теория звукоряда, наиболее полно сформулированная в конце XIX века Германом фон Гельмгольцем — выдающимся естествоиспытателем и философом. Гельмгольц получил огромный экспериментальный материал по ощущению звуков, свел воедино и проанализировал существующие тогда представления о природе музыкальности. В своем фундаментальном труде "Об ощущении тонов как физиологическом основании теории музыки" он выделил три уровня музыкальной акустики: физический (свойства звучания), физиологический (ощущение звука) и психологический (восприятие звука). "Однако именно в области физиологии — точнее, в теории слуховых ощущений — должна теория музыки искать основания своей структуры", — писал Гельмгольц. Большой авторитет Гельмгольца в научном мире привел к тому, что до сих пор его выводы многими музыковедами считаются бесспорными и окончательными.
"ЗООЛОГИЯ" ЗВУКОРЯДОВ
Казалось бы, раз есть натуральный звукоряд, достаточно раз и навсегда указать музыкальные звуки — и дальше заниматься лишь их комбинированием. Однако в музыкальной практике известно огромное количество различных звукорядов — и процесс их порождения продолжается до сих пор. Еще в IV веке до нашей эры утвердилась (приписываемая Пифагору) идея о происхождении всех музыкальных звуков из совершенных консонансов: вверх и вниз от ноты ля первой октавы откладывались квинтовые интервалы; перенос получающихся звуков на одну или несколько октав давал новые допустимые звуки, эквивалентные исходному. Пифагоров строй содержит, как и натуральный, бесконечное число звуков. Однако идея "квинтовых рядов" оказалась весьма продуктивной. Впоследствии на основе "вырезания" части квинтового ряда и октавных перемещений возникали так называемые "математические строи": Царлино (XVI век) — 16 ступеней; Дони (1635) — 20 ступеней; Меркатор (1725) — 53 ступени; Нейдгардт (1718) — 24 ступени... Появлялись такого рода строи и в XIX, и в XX веке.
Однако пифагоров строй в чистом виде может существовать лишь в условиях одноголосья — такие важные для гармонии интервалы, как малая и большая терции, не могут быть получены из квинтового ряда в сколько-нибудь приемлемом приближении. Попытка построить звукоряд на основе большой терции была предпринята во II веке нашей эры Дидимом. В XVI–XVII веках на основе октавы, квинты и большой терции развивался так называемый "чистый строй". Однако музыка в своем развитии требовала значительной гибкости от звукоряда: надо было, чтобы любой допустимый интервал можно было бы отложить от любой ступени звукоряда и получить при этом снова ступень звукоряда — требование регулярности. Математические строи могли удовлетворить это требование лишь для ограниченного числа тональностей и только приближенно. Можно легко показать, что построение регулярного звукоряда вообще невозможно на основе натуральных интервалов. В 1636 году Марен Мерсенн указал, что для регулярности требуется разбиение октавы на равные по величине интервалы — и предложил ряд "равномерно темперированных" звукорядов, с 12, 31 и 26 ступенями. К началу XVIII века относится установление в музыкальной практике 12-ступенного темперированного звукоряда. С этого времени все попытки построения новых звукорядов так или иначе используют требование "темперированности", то есть регулярности.
В 12-ступенном (для краткости будем в дальнейшем опускать слово "темперированный") строе октава (интервал величины 1.000) делится на 12 одинаковых частей — полутонов, соответствующих интервалу малой секунды. Один тон имеет величину равную двум полутонам и соответствует интервалу большой секунды. Любые другие интервалы измеряются целым числом полутонов: малая терция — 3, большая терция — 4, кварта — 5, квинта — 7 и т. д. Обращение (дополнение до октавы) какого-либо интервала сводится к вычитанию его величины в полутонах из 12. Простота этой системы способствовала ее укоренению в среде музыкантов. Как видно, все интервалы 12-ступенного строя (кроме октавы) отличаются от натуральных интервалов (например, натуральная квинта = 0.585, а "темперированная" квинта = 7 / 12 = 0.583), однако в большинстве случаев это не вызывает особого беспокойства. Тем не менее, иногда композиторы ощущают невозможность исполнить те или иные интонации на темперированных инструментах, вроде фортепиано или гитары. Как правило, это происходит при неявном использовании в процессе композиторского творчества других звукорядов, многие из которых неоктавны. Например, последовательность звуков через секундовый интервал (так называемая целотонная гамма) в 12-ступенном строе замыкается через 6 шагов (образуется интервал октавы по отношению к исходному звуку). Однако звучание этой последовательности предполагает, что ее седьмая ступень лежит чуть ниже октавного удвоения первой! То же самое происходит в гаммах "тон–полутон" и ряде других. Другая трудность 12-ступенного строя — исполнение альтерированных звуков. Например, нота до-диез получается поднятием ноты до на полутон, а нота ре-бемоль — опусканием ноты ре на полутон. В 12-ступенном строе это будет одна и та же ступень звукоряда, хотя музыканты чувствуют, что до-диез лежит чуть ближе к ре, а ре-бемоль — ближе к до.
Как ответ на эти противоречия возникают многочисленные темперированные строи с самым различным числом ступеней — вплоть до нескольких сотен! Произвольность конструирования звукорядов позволяет сделать все что угодно, однако порождаемые таким образом конструкции оказываются слишком абстрактными и лишенными каких-то своих специфических черт, которые подсказывали бы, как и где следует применять построенный звукоряд.
ЧТО ЖЕ МЫ СЛЫШИМ НА САМОМ ДЕЛЕ?
Построение натурального звукоряда, либо "математических" строев предполагает, что каждая гармоника составного звука имеет строго определенную частоту, то есть воспринимаемый сигнал имеет линейчатый спектр (см. Рис. 1). Но абсолютно узких линий в природе не бывает. Реально каждая гармоника слегка (а иногда и значительно) "размазана" около некоторой средней частоты. На это обратил внимание еще Гельмгольц, и он же предложил описывать "размытость" тона гауссоидой — распределением частот, которое характеризуется "центром распределения" (соответствующим положению гармоники, ее высоте) и дисперсией (определяющей ширину распределения). Выдающийся советский ученый Н. А. Гарбузов пошел дальше и сформулировал концепцию зонной природы любых музыкальных восприятий. На материале большого числа экспериментов было показано, что звуковысотность, гармония, тембр, темп и ритм, динамика и интонационность — все это воспринимается зонным образом, то есть отклонения физических параметров звучания в ту или иную сторону не влияют, до определенного предела, на качество воспринимаемого звука. Например, в восприятии высоты звука зоны могут быть шире 12-ступенного полутона! Этот результат практически отвергает любые попытки комбинаторного объяснения возникновения звукорядов. Критерии консонанса тоже оказываются подвешенными в пространстве — ибо о каком отношении малых чисел может идти речь, если небольшое изменение одной из частот мгновенно приводит к отношению очень больших чисел! Например,
(3 + 0.001) : (2 + 0.001) = 3001 : 2001 ,
а воспринимается этот интервал все равно как 3 : 2.
|
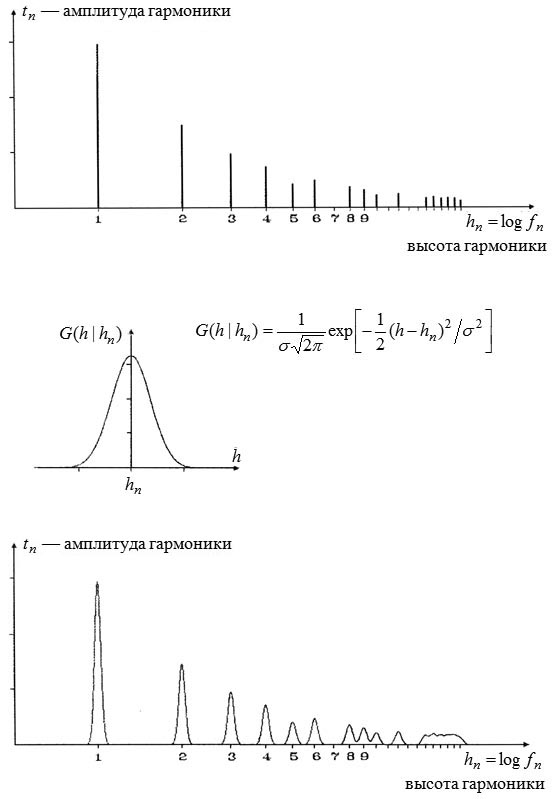
Рис. 1.
Вверху:
Абстрактный тембр — набор высот гармоник и их амплитуд; высоты определяются как логарифмы частот гармоник: fn = nf1 → hn = log fn ; некоторые гармоники при этом могут отсутствовать (амплитуда tn = 0).
Посредине:
Реальная гармоника — гауссово распределение высот около некоторой центральной высоты; ширина распределения определяется величиной дисперсии σ.
Внизу:
Реальный тембр, в котором каждая гармоника "размазана" около своей высоты, а "высота" соответствующей гауссоиды пропорциональна амплитуде tn . Видно, что высшие гармоники сливаются; однако мозг все же умеет выделять их, благодаря наличию установки, то есть предположения о существовании гармоники в определенном месте.
|
Значительно изменились во второй половине XX века представления о работе слухового анализатора. Если раньше считалось, что число воспринимаемых обертонов сравнительно мало из-за интерференции зон возбуждения в улитке уха, то теперь известны особые механизмы для восприятия формы звуковых колебаний, которая определяется сильно высокочастотной частью спектра. Появились данные о компенсации нелинейных искажений в слуховом канале — и о нелинейной обработке сигналов центральной нервной системой. Было экспериментально показано, что в процессах восприятия звуковысотности значительную роль играют высшие отделы мозга.
Наконец, развитие психологической теории деятельности привело к концепции активного участия субъекта в процессах восприятия, нетождественности ощущения и воспринимаемого образа, зависимости восприятия от ситуации. Мы слышим не то, что мы слушаем, — а, скорее, то, что мы предполагаем услышать. Нужны специальные усилия, чтобы перейти от одной установки восприятия к другой.
ВОСПРИЯТИЕ ЗВУКА: ИНФОРМАЦИОННАЯ МОДЕЛЬ
Как описать восприятие звука с участием внутренней, субъективной установки? Если ограничиться пока восприятием отдельных тонов (без гармоник), то естественно предположить, что восприятию некоторого тона — то есть распределения частот вокруг заданной высоты (Рис. 1) — предшествует восприятие другого тона, на который теперь восприятие и настроено. Поэтому новый тон воспринимается как модификация установочного, опорного — небольшой сдвиг с сохранением дисперсии (Рис. 2). Сила влияния нового тона на установочный может быть охарактеризована количеством информации, содержащимся в сдвинутом тоне по отношению к исходному. Эту величину можно рассчитать, и оказывается, что она зависит лишь от квадрата расстояния между звуками по шкале высот и дисперсии распределения (Рис. 3). Смысл ее — субъективное "противоречие" одного звука другому, несовместность звуков. Поэтому и называется она диссонированием. Разумеется, это еще не то, что в музыке обычно понимается под диссонансом, однако именно диссонирование является основой для нахождения отношений между реальными звуками. Пара гармоник максимально "диссонирует" при расстоянии между ними, равном дисперсии. Малое отличие нового тона от старого не несет информации, и потому очень близкие тона "не диссонируют". Субъективно слишком разные сигналы никак не связаны в мозгу друг с другом и потому не мешают один другому, то есть диссонирование близко к нулю.
|
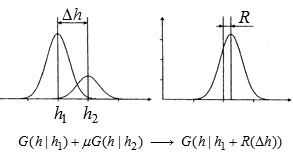
Рис. 2.
На фоне установки G(h1) появление еще одного тона G(h2) воспринимается как "примешивание" его к установочному тону с каким-то малым коэффициентом μ. В результате исходное распределение слегка сдвигается, а величина сдвига R может быть вычислена. Такой сдвиг распределения несет некоторую информацию, которую легко рассчитать; оказывается, что она зависит только от абсолютной величины расстояния между тонами — то есть неважно, который из них является установочным! Коэффициент смешивания μ из дальнейших расчетов выпадает и не влияет на формирование звукорядов.
|
|
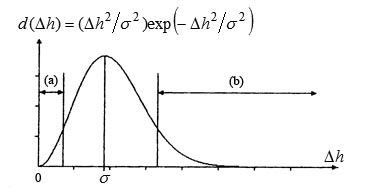
Рис. 3.
Функция диссонирования для отдельных гармоник. Противоречие одного звука другому максимально, когда они находятся на расстоянии примерно равном дисперсии гармоник σ. В области очень малых расстояний (a) звуки слишком похожи, и их взаимодействие не дает новой информации; при больших расстояниях, в зоне (b), звуки просто никак не связаны и существуют независимо друг от друга — с этим эффектом связана возможность разделения в музыке фактурных пластов.
|
Таким образом, обращение к восприятию звука, а не к его ощущению, дает возможность сразу учесть и "размазанность" спектра гармоник, и зонный характер восприятия, и наличие установок. При этом не требуется специального конструирования звукоряда — он получается как результат информационных процессов в мозгу. Расчеты показывают, что возможны лишь звукоряды с приблизительно целым числом ступеней на октаву, а отклонения от октавности соответствуют известным в музыкальной практике свойствам звукорядов. Наиболее устойчивыми и регулярными оказываются звукоряды из 5, 7, 12 и 19 ступеней. Первые три из них соответствуют широко известным в музыке системам пентатоники, диатоники и 12-ступенной темперации, причем в случае 5 и 7 ступеней воспроизводятся существующие в музыкальной практике интервалы между ними, близкие к интервалам натурального строя. 12- и 19-ступенные звукоряды, с учетом зонного характера, оказываются темперированными.
Сложные звуки состоят из набора гармоник-гауссоид, с разными амплитудами. Это внутренний (субъективный) тембр звука. Как указывал Н. А. Гарбузов, внутренний тембр не совпадает с тембром реального звучания. Он описывает еще один уровень субъективной установки: каждому возможному звукоряду отвечает свой внутренний тембр и свое значение дисперсии. При этом дисперсия обратно пропорциональна числу ступеней звукоряда на октаву (которое вовсе не обязано быть целым), а возможные внутренние тембры могут быть получены теоретически из соображений устойчивости по отношению к нелинейным преобразованиям в центральной нервной системе и максимальной регулярности соответствующего звукоряда.
Зная, как взаимодействуют между собой отдельные гармоники, можно рассчитать диссонирование и для пары сложных звуков. Если один звук зафиксировать, а высоту другого плавно изменять, то получится функция диссонирования, наподобие изображенной на Рис. 4. Сразу видно, что эта функция имеет набор минимумов — и тем самым выделяется конечное число звуков, меньше всего диссонирующих между собой. Мозг осуществляет это выделение, просто вычитая из функции диссонирования некоторый средний уровень, плавно изменяющийся на протяжении октавы. В результате образуется набор зон, которые и представляют собой звукоряд (Рис. 4, внизу).
|
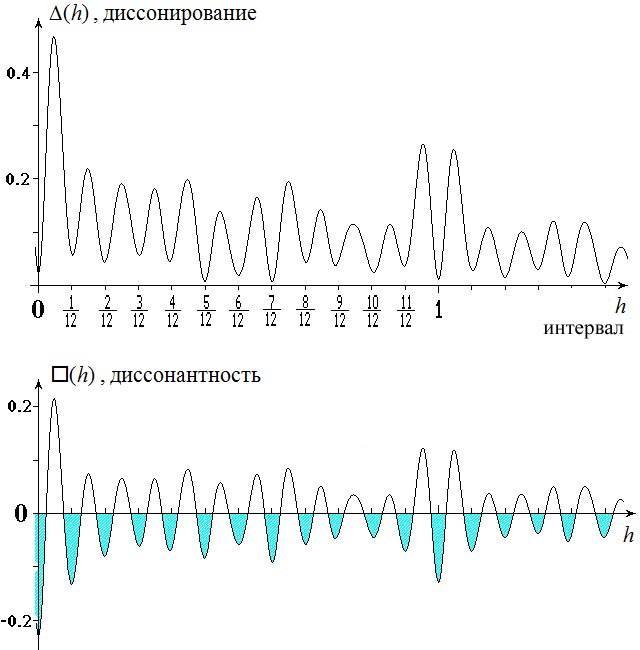
Рис. 4.
Вверху: Функция диссонирования для сложных звуков; внутренний тембр (установка) и дисперсия соответствуют обычному 12-ступенному звукоряду. Заметны минимумы диссонирования в окрестности ступеней звукоряда.
Внизу: Функция диссонантности для 12-ступенного звукоряда. Эта функция определяет возможность принадлежности какого-либо звука зонной структуре, порождаемой функцией диссонирования: если диссонантность меньше нуля, то звук принадлежит соответствующей зоне, то есть консонирует в данном звукоряде, — в противном случае он диссонирует по отношению к этой структуре. Зоны звукоряда на рисунке заштрихованы. Как и ожидалось, на октаву приходится 12 зон.
|
Еще одним "побочным продуктом" информационной модели восприятия высоты звуков является формантная структура внутренних тембров. Субъективно тембр — это не сплошная последовательность гармоник, а отдельные блоки, форманты, — в полном соответствии с известными формантами звуков речи. И как речевые форманты определяют фонемы, так формантная структура внутреннего тембра (звукорядной установки) характеризует специфику и возможности использования соответствующего звукоряда. Можно указать, в каких звукорядах преобладает мелодическое движение, а в каких устанавливается преимущественно гармонический склад. В каждом звукоряде свой набор интервалов, которые могут звучать в аккордовой вертикали — и характерных мелодических ходов. Возможно также описать соотношение "диатонических" и "хроматических" (альтерированных) интервалов.
Исследование изменения формантной структуры внутренних тембров позволяет по-новому взглянуть на историю развития звуковых систем в музыке. При этом оказывается, что в целом развитие музыкального слуха характеризуется увеличением чувствительности — понижением дисперсии гармоник и ростом воспринимаемого их числа. В настоящее время еще есть возможность освоения звукорядов с увеличенным набором ступеней (например, 19) — однако процесс этот не бесконечен, и далеко не всякий звукоряд с числом ступеней больше 12 может существовать как целостное образование.
ИЕРАРХИЯ ЗВУКОРЯДА
Звукоряд — это самостоятельный объект, он живет по своим законам, а не является лишь приближением для каких-то избранных интервалов. Поэтому нельзя передать в музыке, исполняемой в рамках данного звукоряда, такие музыкальные структуры, которые ему не свойственны. Например, представителям современной сериальной музыки приходится прилагать массу усилий, чтобы избежать ассоциаций с интонациями обычной тональной музыки. Звуки 12-ступенного звукоряда по-своему связаны между собой и не дают связывать их по-другому. Для установления новых связей требуется переход к другому звукоряду. Основатель додекафонии Арнольд Шенберг писал: "...несомненно, мы можем соединить двенадцать звуков между собой, но это соединение должно вытекать из уже существующих связей между этими двенадцатью тонами".
Но как определить, какие именно структуры возможны в данном звукоряде? Традиционная теория музыки не дает ответа на этот вопрос, ограничиваясь перечислением эмпирически найденных возможностей. Оказывается, что в информационной модели восприятие звукоряда является иерархичным, то есть звукоряд формируется вместе со всеми возможными в нем структурами. Для их выделения достаточно настроиться, в рамках фиксированной звукорядной установки, на другое число ступеней в октаве (или, что то же самое, изменить дисперсию). Если структура с такой дисперсией существует, то она сразу же появится, представленная своим набором зон и своим характеристическим тембром, описывающим ее свойства! При этом возможно как выделение подструктур (иерархия вложений звукорядов), так и небольшое увеличение числа ступеней звукоряда (что объясняет возможность исполнения некоторых произведений додекафонической музыки на инструментах с 12-ступенной темперацией — и дает генетический механизм перехода от одной музыкальной системы к другой).
Наиболее интересны вложения звукорядов. Для 12-зонного строя возможны подструктуры с 7, 5, 3 и 2 ступенями (Рис. 5). Легко видеть, что 7- и 5-ступенные вложения соответствуют обычным диатоническим и пентатоническим ладам. Структура из трех нот соотносится с мажорным и минорным трезвучиями — основой тональной музыки. Наличие структуры из двух нот подчеркивает особую роль квинтового интервала — как это исторически и сложилось в музыке. Таким образом, исследование процессов восприятия высоты звука естественным образом приводит к уже известным музыкальным фактам. Дальше уже можно анализировать различные варианты соотношения структур различных уровней между собой. Например, возможны их взаимные сдвиги по шкале высот: скажем, мажорное трезвучие не обязательно строится на основной ступени лада, тонике. Кроме того, основной тон лада не обязательно совпадает с опорным звуком, по отношению к которому строится функция диссонирования и к которому "привязана" система зон. Так появляются различные разновидности диатонических ладов, обращения аккордов и т. п. В результате звук, принадлежащий одной подструктуре, может не принадлежать какой-либо другой. Например, есть ступени звукоряда, не входящие в лад — отсюда понятие альтерации ступеней лада и хроматических интервалов (набор возможных хроматических ходов определяется формантной структурой внутреннего тембра). С другой стороны, внеладовые звуки вполне могут быть ступенями некоторого аккорда. Естественно тогда определить консонанс как принадлежность звука некоторой зонной структуре, а диссонанс — как выход за ее пределы. Видно, что понятия консонанса и диссонанса оказываются относительными: звук может консонировать в аккорде — но быть ладовым диссонансом, и наоборот. Возникающая из-за этого игра тяготений широко используется композиторами для модуляций из одной тональности в другую и создания эффекта напряженности звучания. Мы еще раз убеждаемся в большей правильности и естественности описания свойств музыкального звука на уровне восприятия, а не на уровне ощущения.
|
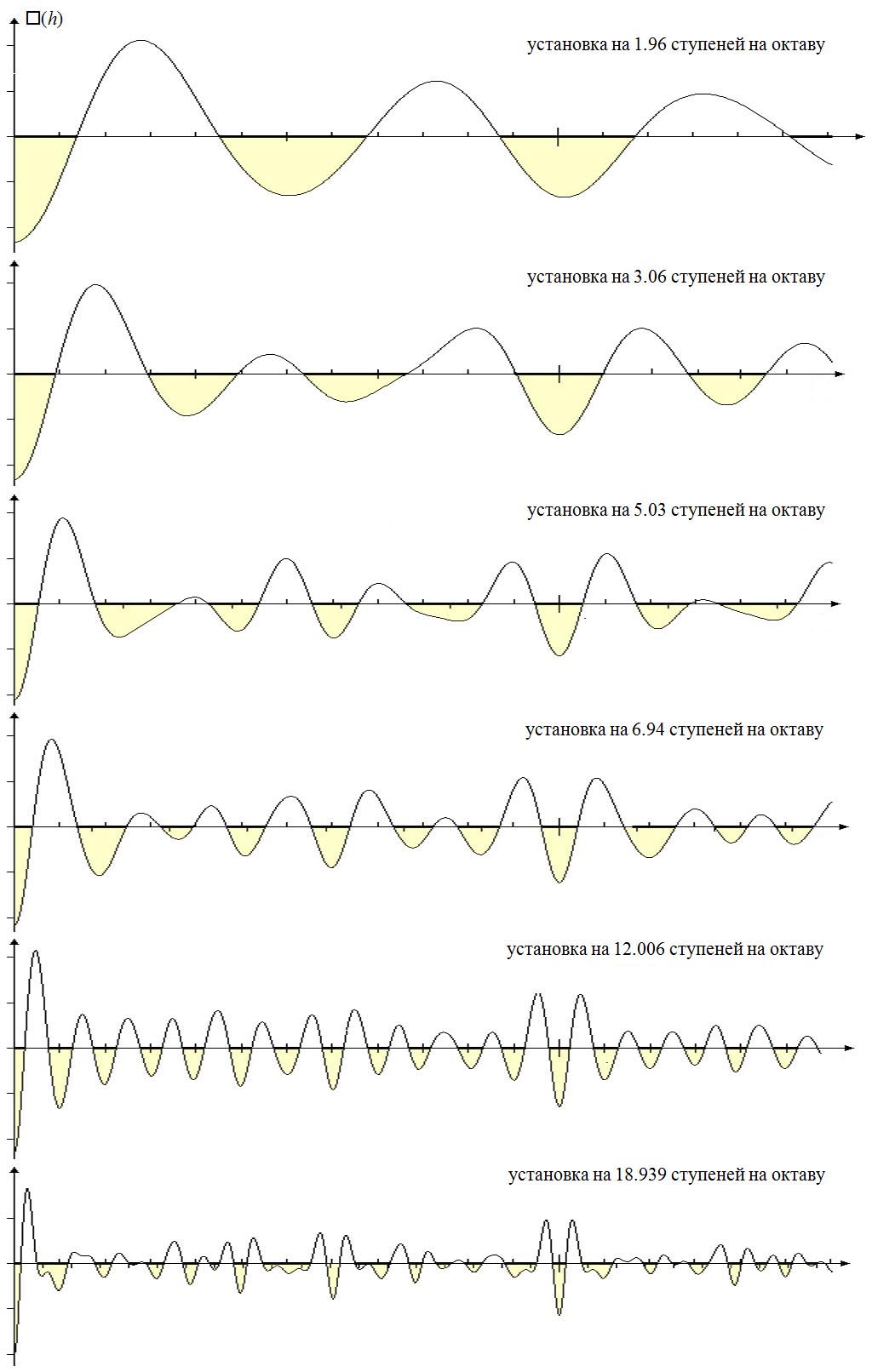
Рис. 5.
При фиксированной установке на 12-зонный строй возможны, в зависимости от музыкального контекста различные уровни "подробности" восприятия соответствующей функции диссонирования. В 12-ступенном звукоряде существуют структуры, изображенные на рисунке. Наряду с основным "ритмом", 12 зон на октаву, выделяются также подструктуры из трех, пяти и семи зон. Все эти структуры представлены в психике одновременно и образуют иерархию звукорядных вложений, описывающую такие уровни музыки как лад и гармония. Существует также возможность частичного восприятия ритмов с числом зон, превышающим 12. Ближайшая возможность — 19 ступеней. Однако при установке на 12-ступенный звукоряд некоторые зоны 19-ступенного строя сливаются. Полное выделение 19-зонного строя возможно лишь при формировании отвечающей ему тембровой установки.
|
Поскольку все звукоряды на всех уровнях (вложениях) имеют зонную природу, возникает возможность при исполнении музыки подчеркивать те или иные интонации, изменяя высоту звука в пределах зоны. Так на практике и поступают исполнители высокого класса. При этом в зависимости от художественных задач используются либо звукорядные зоны, либо зоны ладового уровня, либо зоны на уровне гармонии. Поскольку на более высоких уровнях зоны гораздо шире, вариация, скажем, ступени лада может достигать величин, сравнимых с расстоянием между ступенями звукоряда (больше 12-ступенного полутона). Такого рода явления типичны для некоторых форм восточной музыки, имеющих звукоряды, отличные от 12-ступенного. В частности, интонационное варьирование может привести к возникновению звукорядных диссонансов, то есть к выходу за рамки текущей звукорядной установки. Результатом такого выхода становится значительная неустойчивость звучания, требующая либо незамедлительного разрешения в одну из ступеней звукоряда, либо перестройки самого звукоряда. Так, через развитие интонирования происходит постепенное изменение звукорядных представлений в истории музыки.
По-видимому, ближайшим направлением такого расширения представлений о звукорядности станет практическое освоение 19-зонного строя. По своим характеристикам этот строй не уступает 12-ступенному: хорошо сбалансированные мелодика и гармония, устойчивость, регулярность, артикулированность. 19-зонный строй является хорошо темперированным и имеет развитую иерархию вложений. Особенностью этого звукоряда является несколько пониженная квинта, очень мягко и насыщенно звучащая в аккордах. В результате снимаются некоторые ограничения на технику полифонии, а расширенный набор гармонических (то есть применяемых в гармонии) интервалов позволяет значительно обновить арсенал выразительных средств композитора. В частности, имеющиеся подструктуры из четырех нот отвечают септаккордам, причем в них прекрасно звучит натуральная септима (отношение 7 : 4), отсутствующая в 12-ступенном строе. С другой стороны, наличие 7- и 3-ступенных вложений позволяет исполнять в 19-зонном строе обычную тональную музыку — причем иногда ближе к замыслу композитора. Действительно, на Рис. 6, показано расположение клавиш 19-ступенного фортепиано. Интервалу большой секунды соответствует интервал из трех ступеней 19-ступенного звукоряда, а малой секунде — интервал из двух ступеней. В результате до-диез оказывается выше, чем ре-бемоль, — а так и должно быть в соответствии с их ладовыми функциями! Кроме того, появляется еще один вариант "полутона", величиной в одну ступень звукоряда. Он прекрасно соответствует так называемому вводному полутону, который невозможно передать на инструментах с фиксированной 12-ступенной настройкой. Естественно моделируются в 19-зонном строе целотонная гамма и гаммы типа "тон–полутон", о трудностях исполнения которых уже говорилось.
|
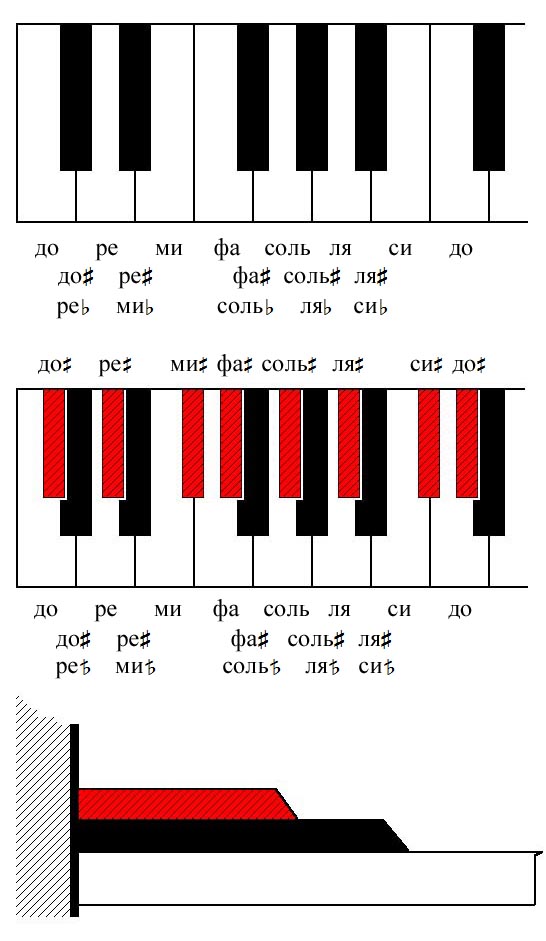
Рис. 6.
Вверху: Обычная клавиатура фортепиано, в пределах октавы. Всего на октаву приходится 12 клавиш; интервал между любыми двумя соседними клавишами равен 12-ступенному полутону. Белые клавиши образуют диатонический 7-ступенный звукоряд и отвечают вложению 7 → 12; черные клавиши расположены по ступеням пентатоники и соответствуют вложению 5 → 12. Повышение диатонической ступени обозначается знаком 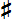 (диез); понижение диатонической ступени обозначается знаком (диез); понижение диатонической ступени обозначается знаком 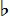 (бемоль). (бемоль).
Внизу: Клавиатура 19-ступенного фортепиано. По сравнению с обычной клавиатурой, появляется дополнительный ряд клавиш, который удобно выделить цветом (например, красным) и немного приподнять над уровнем черных клавиш — аналогично тому, как на обычной клавиатуре черные клавиши выше уровня белых. Белые клавиши по-прежнему отвечают диатоническому звукоряду, а черные — пентатонике; однако имеется еще одна диатоническая гамма — по "красным" клавишам. Повышение на одну ступень 19-ступенного звукоряда обозначается знаком 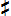 (полудиез), а повышение на две ступени — знаком (полудиез), а повышение на две ступени — знаком 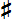 (диез). Аналогично, понижение на одну ступень обозначается знаком (диез). Аналогично, понижение на одну ступень обозначается знаком 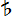 (полубемоль), а на две ступени — знаком (полубемоль), а на две ступени — знаком 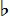 (бемоль). Целый тон (интервал между до и ре) в 19-ступенном звукоряде содержит 3 ступени звукоряда; полутон (расстояние между ми и фа) содержит 2 ступени. Кроме этого, имеется вводный полутон — интервал в одну ступень звукоряда. Такого рода вводные интервалы широко применяются в музыке, однако плохо передаются на темперированных 12-ступенных инструментах. (бемоль). Целый тон (интервал между до и ре) в 19-ступенном звукоряде содержит 3 ступени звукоряда; полутон (расстояние между ми и фа) содержит 2 ступени. Кроме этого, имеется вводный полутон — интервал в одну ступень звукоряда. Такого рода вводные интервалы широко применяются в музыке, однако плохо передаются на темперированных 12-ступенных инструментах.
|
Однако применение 19-ступенного звукоряда не сводится к обогащению уже имеющихся средств тональной музыки. В его иерархии вложений существуют целостные образования из 12 звуков, которые, по аналогии с 12-ступенным строем, можно было бы назвать гиперладами. Например, гиперлад, состоящий из 1, 3, 5, 6, 8, 9, 11, 12, 14, 16, 17, и 19 ступеней не содержит в себе диатонических (7-ступенных) ладов и может служить основой для "тональной додекафонии", о которой размышлял А. Шенберг. Наличие естественных связей в гиперладе приводит к легкому закреплению его в памяти и к быстрому узнаванию характерных только для него интонаций. "Аккорды" в гиперладах строятся не на основе трезвучия, как в обычной тональной музыке, а на основе структур из пяти звуков, резко отличающихся по составу от традиционной пентатоники.
Заметим, что переход к 19-ступенному звукоряду приводит лишь к небольшому изменению существующих музыкальных инструментов и не требует какой-либо иной техники исполнения. Это еще одно достоинство строя, позволяющее широко распространить его в практике. Конечно, исполнение на скрипке потребует настройки ее по "гармонизированным" (19-ступенным), а не по чистым квинтам. Однако эти квинты обладают очень характерным, легко воспроизводимым звучанием — так что при небольшом навыке проблем здесь не возникает. Пение в 19-ступенном строе гораздо легче для непрофессионала, чем 12-ступенное интонирование, требующее предварительной постановки голоса. И хотя некоторые мелодии теряют кристальность классического бельканто, интонация становится мягче и ближе к речевой, приобретает новые оттенки.
ЧТО ПОТОМ?
Разумеется, развитие музыкальной практики гораздо богаче, чем простая смена одних звукорядных представлений другими. Скорее всего, использование того или иного звукоряда будет более осознанным, зависящим от художественной задачи. Однако это обязательно потребует более глубокого понимания законов восприятия звуковысотности. В какой-то мере такое понимание развивается иерархической информационной моделью восприятия, о которой шла речь в этой заметке. Но есть уже в современной музыке тенденции, не вписывающиеся в рамки модели. Активное привлечение компьютерной техники на этапе сочинения музыки, появление музыкальных компьютеров как принципиально новых инструментов, наконец, появление новых синтетических жанров — все это потребует специального осмысления. Нужно еще понять, как сливаются в музыкальной интонации звуковысотность и ритм, как происходит переход к сплошному спектру сигнала, не расчленяемому на комплексы гармоник. Однако в любом случае необходимо понимать музыкальное восприятие как иерархию деятельностей, как активное конструирование представлений, а не простое коллекционирование ощущений, сколь бы детальными они ни были.
|